PHYSICAL PROPERTIES OF AIR

1- І PROBLEMS OF AIRPLANE AERODYNAMICS

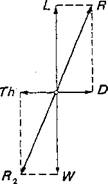
An airplane moves in the earth’s atmosphere. The state of motion of an airplane is determined by its weight, by the thrust of the power plant, and by the aerodynamic forces (or loads) that act on the airplane parts during their motion. For every state of motion at uniform velocity, the resultant of weight and thrust forces must be in equilibrium with the resultant of the aerodynamic forces. For the particularly simple state of motion of horizontal flight, the forces acting on the airplane are shown in Fig. 1-1. In this case, the equilibrium condition is reduced to the requirement that, in the vertical direction, the weight must be equal to the lift (W = L) and, in the horizontal direction, the thrust must be equal to the drag (Th =D). Here, lift L and drag D are the components of the aerodynamic force Rx normal and parallel, respectively, to the flight velocity vector V. For nonuniform motion of the aircraft, inertia forces are to be added to these forces.

In this book we shah deal exclusively with aerodynamic forces that act on the individual parts, and thus on the whole aircraft, during motion. The most important parts of the airplane that contribute to the aerodynamic forces are wing, fuselage, control and stabilizing surfaces (tail unit or empennage, ailerons, and canard surfaces), and power plant. The aerodynamic forces depend in a quite complicated manner on the geometry of these parts, the flight speed, and the physical properties of the air (e. g., density, viscosity). It is the object of the study of the aerodynamics of the airplane to furnish information about these interrelations. Here, the following two problem areas have to be considered:

1. Determination of aerodynamic forces for a given geometry of the aircraft (direct problem)

2. Determination of the geometry of the aircraft for desired flow patterns (indirect problem)

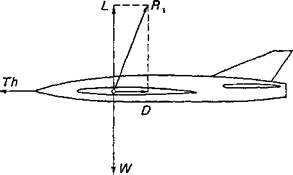Figure 1-1 Forces (loads) on an air­plane in horizontal flight. L, lift; D, drag; W, weight; Th, thrust; R1, re­sultant of aerodynamic forces (result­ant of L and D); R2, resultant of W and Th.

The object of flight mechanics is the determination of aircraft motion for given aerodynamic forces, known weight of the aircraft, and given thrust. This includes questions of both flight performance and flight conditions, such as control and stability of the aircraft. Flight mechanics is not a part of the problem area of this book. Also, the field of aeroelasticity, that is, the interactions of aerodynamic forces with elastic forces during deformation of aircraft parts, will not be treated.

The science of the aerodynamic forces of airplanes, to be treated here, forms the foundation for both flight mechanics and many questions of aircraft design and construction.

1- 2-1 Basic Facts

In fluid mechanics, some physical properties of the fluid are important, for example, density and viscosity. With regard to aircraft operation in the atmosphere, changes of these properties with altitude are of particular importance. These physical properties of the earth’s atmosphere directly influence aircraft aero­dynamics and consequently, indirectly, the flight mechanics. In the following discussions the fluid will be considered to be a continuum.

The density q is defined as the mass of the unit volume. It depends on both pressure and temperature. Compressibility is a measure of the degree to which a fluid can be compressed under the influence of external pressure forces. The compressibility of gases is much greater than that of liquids. Compressibility

therefore has to be taken into account when changes in pressure resulting from a particular flow process lead to noticeable changes in density.

Viscosity is related to the friction forces within a streaming fluid, that is, to the tangential forces transmitted between ambient volume elements. The viscosity coefficient of fluids changes rather drastically with temperature.

In many technical applications, viscous forces can be neglected in order to simplify the laws of fluid dynamics (inviscid flow). This is done in the theory of lift of airfoils (potential flow). To determine the drag of bodies, however, the viscosity has to be considered (boundary-layer theory). The considerable increase in flight speed during the past decades has led to problems in aircraft aerodynamics that require inclusion of the compressibility of the air and often, simultaneously, the viscosity. This is the case when the flight speed becomes comparable to the speed of sound (gas dynamics). Furthermore, the dependence of the physical properties of air on the altitude must be known. Some quantitative data will now be given for density, compressibility, and viscosity of air. Material Properties

Density The density of a gas (mass/volume), with the dimensions kg/m3 or Ns2/m4, depends on pressure and temperature. The relationship between density q, pressure p, and absolute temperature T is given by the thermal equation of state for ideal gases

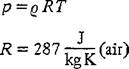(l-lc)

(1-1£) where R is the gas constant. Of the various possible changes of state of a gas, of particular importance is the adiabatic-reversible (isentropic) change in which pressure and density are related by

P

— = const

Here 7 is the isentropic exponent, with

(1-Зя)

= 1.405 (air)

cp and cv are the specific heats at constant pressure and constant volume, respectively.

Very fast changes of state are adiabatic processes in very good approximation, because heat exchange with the ambient fluid elements is relatively slow and, therefore, of negligible influence on the process. In this sense, dow processes at high speeds can usually be considered to be fast changes of state. If such flows are steady, isentropic changes of state after Eq. (1-2) can be assumed. Unsteady-flow

processes (e. g., with shock waves) are not isentropic (anisentropic); they do not follow Eq. (1-2).

Across a normal compression shock, pressure and density are related by

(7-1)+ (7+ 1) —

(h _____________________ El

Qi Pt

(7 + 1) + (7 — l)~r Pi

7+1

<-—r = 5.93 (air)

7 — I v ‘

where the indices 1 and 2 indicate conditions before and behind the shock, respectively.

Speed of sound Since the pressure changes of acoustic vibrations in air are of such a high frequency that heat exchange with the ambient fluid elements is negligible, an isentropic change of state after Eq. (1-2) can be assumed for the compressibility law of air: p{q). Then, with Laplace’s formula, the speed of sound becomes

a = ]/7 RT 0‘5fl)

a0 = 340 m/s (air) (1 -5 b)

where for pie the value given by the’ equation of state for ideal gases, Eq. (1-lar), was taken. Note that the speed of sound is simply proportional to the square root of the absolute temperature. The value given in Eq. (1 -5b?) is valid for air of temperature t = 15°C or T = 288 K.

Viscosity In flows of an inviscid fluid, no tangential forces (shear stresses) exist between ambient layers. Only normal forces (pressures) act on the flow. The theory of inviscid, incompressible flow has been developed mathematically in detail, giving, in many cases, a satisfactory description of the actual flow, for example, in computing airfoil lift at moderate flight velocities. On the other hand, this theory fails completely for the computation of body drag. This unacceptable result of the theory of inviscid flow is caused by the fact that both between the layers within the fluid and between the fluid and its solid boundary, tangential forces are transmitted that affect the flow in addition to the normal forces. These tangential or friction forces of a real fluid are the result of a fluid property, called the viscosity of the fluid. Viscosity is defined by Newton’s elementary friction law of fluids as

du

T=^

Here 7 is the shearing stress between adjacent layers, dujdy is the velocity gradient nor­mal to the stream, and д is the dynamic viscosity of the fluid, having the dimensions Ns/m2. It is a material constant that is almost independent of pressure but, in gases,
increases strongly with increasing temperature. In all flows governed by friction and inertia forces simultaneously, the quotient of viscosity p and density g plays an important role. It is called the kinematic viscosity v, and has the dimensions m2/s. In Table 1-1 a few values for density o, dynamic viscosity ju, and kinematic viscosity v of air are given versus temperature at constant pressure.