SINUSOIDAL DESCRIBING FUNCTION

When a stable linear system has a sinusoidal input x — A1eiat the steady – state output y(t) after the initial transients have decayed is a sinusoid of the same frequency, and the input/output relation is given by (3.4,20). A “well-behaved” nonlinear system with such an input will have a steady-state output that is also periodic, but not sinusoidal, other harmonics being present. Whereas the input spectrum is a “spike,” the output spectrum is a “comb.” Other behavior is conceivable, but the above describes the usual situation; we assume it to be the case here. Since the mean product of sinusoids of different frequency is zero, the only Fourier component of the output that has a nonvanishing correlation Rxy with the input is the fundamental, i. e. the component that has the same frequency £1 as the input.

Since Фху is the Fourier integral of Rxy, it follows that only the funda­mental component yf of у contributes to Фга. From (2.6,22) we have

ФХУі = lim – LX*(im;T)Yf(im;T)

T-+ 00 4:1

Фхх = lim — X*(ia>; Т)Х(ію; T) t-> oo 4T

The ratio (3.5,7) then leads simply to

Щісо) = (3.5,9)

Х(га>)

where Yf(ia>) and X(ia>) are the Fourier transforms of the sinusoids, given in Table 2.2. Now if these sinusoids are described by

x = АіЄг’ш; yf = A2elQt

where Ax and A2 are the complex amplitudes of the input and output fundamental, respectively, we get, using item 3, Table 2.2,

Щісо) = ^ (3.5,10)

■d-i

which is identical with the frequency-response function given by (3.5,20) provided that we regard the fundamental as the total output.

Evidently the sinusoidal describing function leads to a remnant made up of all the lower and higher harmonics of the output.

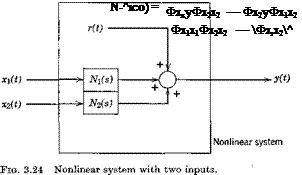
TWO-INPUT DESCRIBING FUNCTIONS

If two inputs to a nonlinear system contribute to the output y, as in Fig. 3.24 we may define two describing functions by the same principle as used

above for one input. The method is basically the same, but the details are a little more involved. The result for Nj is

and that for N2(ico) is obtained by permuting the subscripts 1 and 2. Note that if aq and x2 are uncorrelated, so that the cross-spectral density ФХіХ2 = 0, then (3.5,11) reduces to (3.5,7), the formula for a single input.