THE INFLUENCE OF JET ENGINES

The direct thrust moment of jet engines is treated as shown at the beginning of this section, the constant-thrust idealization given in (3.4,6) often being adequate. In addi­tion, however, there is a normal force on jet engines as well as on propellers.

Jet Normal Force

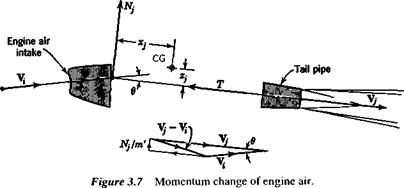
The air that passes through a propulsive duct experiences, in general, changes in both the direction and magnitude of its velocity. The change in magnitude is the prin­cipal source of the thrust, and the direction change entails a force normal to the thrust

line. The magnitude and line of action of this force can be found from momentum considerations. Let the mass flow through the duct be m’ and the velocity vectors at the inlet and outlet be V, and Vr Application of the momentum principle then shows that the reaction on the airplane of the air flowing through the duct is

F = – V,-) + F’

where F’ is the resultant of the pressure forces acting across the inlet and outlet areas. For the present purpose, F’ may be neglected, since it is approximately in the direc­tion of the thrust T. The component of F normal to the thrust line is then found as in Fig. 3.7. It acts through the intersection of V, and V,, The magnitude is given by

Nj = m’Vj sin в

or, for small angles,

Nj = m’Vie (3.4,11)

In order to use this relation, both Vi and в are required. It is assumed that F, has that direction which the flow would take in the absence of the engine; that is, в equals the angle of attack of the thrust line a, plus the upwash angle due to wing induction e;.

6=ctj+ €j (3.4,12)

It is further assumed that the magnitude V, is determined by the mass flow and inlet area; thus

where A, is the inlet area, and p, the air density in the inlet. We then get for Nj the ex­pression

The corresponding pitching-moment coefficient is

Пі’2 X: ■

Дcm = -— 7 (a.- + €/)

Since the pitching moment given by (3.4,14) varies with a at constant thrust, then there is a change in Cma given by

(3.4,15)

The quantities m’ and p, can be determined from the engine performance data, and for subsonic flow, dcj/da is the same as the value дєр/да used for propellers, dxfda can be calculated from the geometry.

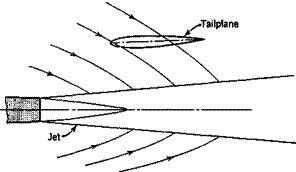
Jet Induced Inflow

A spreading jet entrains the air that surrounds it, as illustrated in Fig. 3.8, thereby inducing a flow toward the jet axis. If a tailplane is placed in the induced flow field, the angle of attack will be modified by this inflow. A theory of this phenomenon which allows for the curvature of the jet due to angle of attack has been formulated by Ribner (1946). This inflow at the tail may vary with a sufficiently to reduce the stability by a significant amount.