Theoretical Model

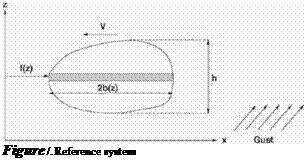The systems discussed will have one degree-of-freedom. They consist of a rigid body, whose position can be described by a single coordinate. The body has a length distribution b(z) in the slreamwise coordinate x, as shown in Fig. 1.

The height of the system is h; f(z) is the local position of the leading edge line. The gust is applied in a direction normal to the plane (ж, z). The fbw model will be potential, with a free stream velocity V in the x-direction. The fbw will be inviscid, subject to small perturbations, created by oscillatory gusts of reduced frequency k.

The gust response will be modeled in the frequency domain by the admit­tance, that we indicate with H(k). In wind engineering, this quantity is often indicated by x2. For a more detailed discussion, see Filippone and Siquier, 2003, Filippone, 2003.

For complete clarity, the admittance is a transfer function defined as the ratio between the loads under unsteady forcing of finite frequency к and the quasi steady loads, e. g. loads with infinitely large wavelength:

where F is a generic load (lift, side force, yaw moment, etc.). With the defi­nition Eq. 1 we have H —> 1 as к —» 0. This definition is coherent with that given originally by Davenport (1961). A result not conforming with this limit­ing value will not be considered correct. The definition of Eq. 1 is important, also because it is related in a straightforward way to the power spectra density:

PSD(k) ~ 2H’k) (2)

which does not require the Fourier transform of the system’s response in the ti me domai n.

In an earlier study (Filippone and Siquier, 2003), we proved that under the above conditions the admittance for side force (or lifting force) can be de­scribed by the following equation:

H(k) = I / r{z)Hx[r{z)k]e-iv{z)kdz (3)

h J h

where

C (k) = F (k) + iG(k). (5)

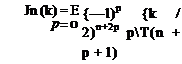The quantities J0, J are Bessel functions of the first and second kind in the reduced frequency k

and Г is the gamma function; A is the gust speed ratio, defined as

where Vg is the gust velocity in a frame of reference fixed with the ground, V is the velocity of the body. All the values of A can be considered, except the singular value obtained for V = —Vg (e. g. when the gust and the body are traveling in opposite directions with the same speed). The value A = 1 corresponds to a stationary gust, e. g. Vg = 0; A = 0 is a limit value obtained with Vg/V ^ ±ro, which is possible with a stationary body (e. g. V = 0) and a moving gust. Values of 0 < A < 1 are the most common in practical applications.

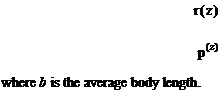Finally, two functions, appearing in Eq. 3 are two functions of the local body length