Topology of the Computed Skin-Friction and Velocity Fields
Before we discuss the computed radiation-adiabatic temperature fields, we need to have a look at the topology of the computed skin-friction field. We do this in order to identify in particular attachment and separation lines, where we expect hot-spot, and cold-spot situations, respectively, Sub-Section 3.2.4. Discussed are the results for the large wing with L = 14 m. The skin – friction line topology at the smaller wing is very similar.
Take first a look at the windward side of the configuration. In Fig. 3.16 we see the classical skin-friction line pattern at the lower side of a delta wing. Because the lower side of the BDW is only approximately flat, the flow
|
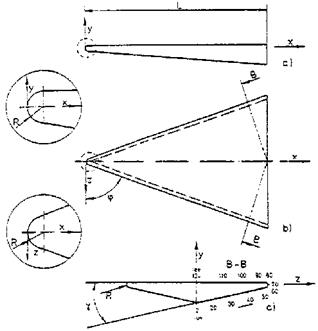
Fig. 3.15. Configuration of the BDW and the employed notation [34]. |
exhibits a slight three-dimensionality between the two primary attachment lines. These lines themselves are marked by strongly divergent skin-friction lines. The stagnation point, which topologically is a singular point, in this case a nodal point, see, e. g., [18], lies also on the lower side, at about 3 per cent body length. The primary attachment lines are parallel to the leading edges almost from the beginning, i. e., they do not show a conical pattern.
The situation is quite different at the leeward side of the wing, Fig. 3.17. Here we see on the left-hand side (from the leading edge towards the symmetry line) a succession of separation and attachment lines: the primary separation line Si, the secondary attachment line A2, a secondary separation line S2, and a tertiary attachment line A3. All is mirrored on the right-hand side of the wing. Again a conical pattern is not discernible, except for a small portion near to the nose. However, the secondary separation lines are almost parallel to the single tertiary attachment line along the upper symmetry line of the wing.
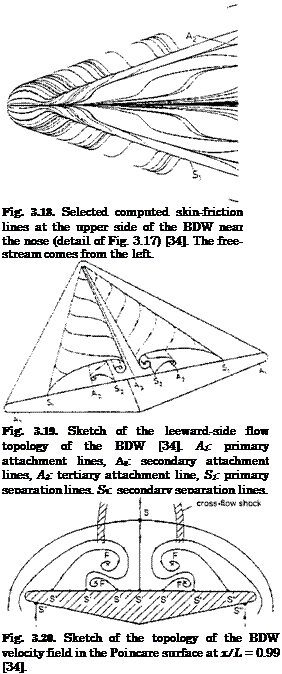
Both the primary and the secondary separation are of the type “open separation”, i. e., the separation line does not begin in a singular point on the surface, as was shown first by K. C. Wang [37]. Fig. 3.18 shows this for the primary separation line.
With these surface patterns we can attempt to construct qualitatively the structure of the leeward-side flow field, Fig. 3.19. By marking the points,
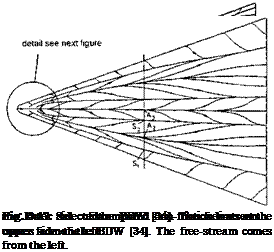
where the streamlines of the vortex-feeding layers penetrate a surface normal to the x-axis, one finds the Poincare surface [38], Fig. 3.20. The computed cross-flow shocks are indicated.
In Fig. 3.20 the attachment and separation lines are marked as “halfsaddles (S’)” (note that the primary attachment lines are “quarter-saddles (S’")”, because the flow between them is (more or less) two-dimensional. The axes of the primary and the secondary vortices are marked as “focal (F)” points, which are counted as “nodal (N)” points. Finally a “saddle (S)” point is indicated above the wing. This pattern obeys the topological rule (see [18])
and therefore is a valid topology.
![]()
Note in particular that at all attachment lines not only the characteristic thickness A is small, but that also the attaching streamlines come from the outer inviscid flow and hence carry the original free-stream total enthalpy. This is in contrast to, for instance, (steady) two-dimensional separation, where the attaching separation layer does not carry the original total enthalpy, if the boundary layer ahead of the separation point is radiation or otherwise cooled.