Transonic Small Disturbance Theory

4.1.1 Governing Equation

Assuming inviscid, steady, 2-D flow of perfect gas, the Euler equations are perturbed about a uniform flow near Mach one. In this section for practical reasons, we will use dimensionless perturbation velocity components (u, w) defined as

Vx = и (1 + u), Vz = U w (4.55)

where ~V is the total velocity. With this notation, the Euler equations read

dpU(1+u) , dpUw 0

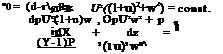dx + dz = 0

Note that the energy equation has been replaced by the constant enthalpy condi­tion, valid for isoenergetic flows, even when shocks are present. For a thin airfoil of vanishing camber, thickness or incidence of order є ^ 1, the flow dependent variables are expanded as

p = P0 (1 + є3 p(1) + є3 p(2) +—— )

U (1 + u) = U (1 + є3 u(1) + є 3 u(2) + •••) (4 57)

U w = U (єж(1) + є 3 w(2) + ■■■)

. p = P0 + P0U 2(є3 p(1) + є3 p(2) +——– )

In order to obtain a mixed-type equation in a transformed plane (£ = x, ( = є 3 z), it has been shown that one needs to assume that, as є ^ 0, the Mach number approaches unity, i. e. 1 – M2 = O (є3).

One starts with evaluating the following groupings:

pU(1 + u) = p0U ^1 + є3(p(1) + u(1)) + є3(p(1)u(1) + p(2) + u(2)) + ■■■ ^
pUw = p0U ^w(1) + є3 (p(1)w(1) + w(2)) + ■■■
pU 2(1 + u)2 = p0U2

x (1 + є3 (p(1) + 2u(1)) + є4 (2p(1)u(1) + u(1)2 + p(2) + 2u(2)) + ■■■) pU2(1 + u)w = p0U2 ^w(1) + є3(p(1)w(1) + u(1)w(1) + w(2)) + ■■■ ^ pU2w2 = p0U2 (є2w(1)2 + ■■■)

When these expressions are substituted in the Euler equations, at the lowest order one finds the following results.

For conservation of mass:

For the x-momentum:

The first two PDEs can be integrated as

p(1> + u(1> = F (Z >, p(1> + 2u (1> + p(1> = G (Z > (4.62)

where F and G are arbitrary functions of Z. However, since the perturbations vanish at infinity for all values of Z, F = G = 0. Hence p(1> = —u(1> and p(1> = – u(1>. The z-momentum equation yields a first PDE for (u(1>, w(1>), so that we now have

‘ dw(1> du(1> _ n

Щ—– ЇЇТ = 0

p(1> = —u (1> (4.63)

p(1> = —u(1>

The PDE states that the flow is irrotational at order one, i. e. there exists ф(1> (Z, Z> such that Vф(1> = (u(1>, w(1>). In order to find a second PDE for (u(1>, w(1>), we need to carry out the expansions to the next order for the PDEs and for the equation of constant enthalpy. Consider first the enthalpy equation. To lowest orders one finds

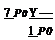
U 2

+ ^ = Я0

є2 – y—ї (y m02 p(1> — p(1> + (y —1> m2 u (1>}

where we have made use of a2 = yp0/p0 and M0 = U/a0. When p(1> and p(1> are eliminated in terms of u(1>, the terms do not balance to zero, but there remains

since, by hypothesis, (1 in the expansion. Let	m2) = O (e 3). This remainder is added to the next term
(4.67)

K is of order unity and is called the transonic similarity parameter. It is defined up to a multiplicative factor Mg, к > 0. Two definitions are commonly used:

K = 1—M0, (Cole)

1-M23 (4.68)

K =——- 0, (Spreiter)

M2 e3

At the next order we now obtain

The right-hand-side must be O(e2) or higher. Again, eliminating p(1) and p(1) in terms of u(1) yields for the unknowns of the level 2 approximation:

Ym2p(2) – p(2) + (y – 1)M2u(2) + Ku(1) + (1 – YM2)u(1) 2 + —1 M2u(1) 2 = O(e3)

(4.70)

Returning now to the conservation of mass and x-momentum

‘ e4 (d(p"u"> + p(2> + u(2)) + ) = 0 (471)

e q | (2p(1)u(1) + u(1) 2 + p(2) + 2u(2) + p(2)) + = 0 )

Subtracting one from the other and substituting p(1) = – u(1) yields

which can be integrated to give p(2) = —u(2). Now, solving the energy equation for p(2) in terms of u(2) and first-order terms provides the following result:

p(2) = – M^u{T) + Ku(1) + ^1 – M02) u(1)2 + O(e2) (4.73)

Final substitution of these expressions in the first PDE above, reduces it to

(4.74)

Note that the first and last terms in the inner bracket are of higher order and can

4

be dropped to give at O (є 3):

In the second-order approximation, the level-2 unknowns p(2), u(2), w(2) and p(2) do not appear, but the nonlinear contribution involving level-1 unknowns remains.

Reverting to the physical variables (x, z), with Cole’s definition of the tran­sonic similarity parameter, the results are the following for the velocity, density and pressure:

U (1 + є2 u(1)) = U (1 + u)

U єю(Г) = U w

2 m (4.76)

P = po(1 + є3p(1)) = po(1 – u)

. p = Po + PoU2є3 p(1) = po – poU2u

Note that now Cp = —2u. The governing equations for (u, w) read

called the Transonic Small Disturbance equation (TSD). In non-conservative form, it reads

Let u* = (дф/дx)* = (1 — m2)/ ((j + 1)M2) represent the critical pertur­bation velocity. The TSD equation is a nonlinear equation of mixed-type. When u = дф/дx < u*, the equation is of elliptic type, which corresponds to subsonic
flow. When u = дф/д x > u*, the equation is of hyperbolic type, which corresponds to supersonic flow. The sonic line is given by u = дф/дx = u*.

The linearized Mach number-u relation is given by

u Y + 1 2

M(u) = M0 + (1 – M0)— = M0 + ^—M^u (4.80)

u* 1 + M0

In the supersonic subdomain, characteristic lines exist. The rigorous full theory of characteristics is beyond the scope of this book (see Appendix C2 for a brief introduction). For further information the reader is referred to Courant and Hilbert, Ref. [1], or also to JJC, [2].

The slopes of the C + and C – characteristics can be found to be:

/ dz_ ________ 1_______ / dz __________________ 1_______

dx’C+ У (y + 1)M02 ju-v*’ dx)c – J(y + 1)

(4.81)

The slopes of the characteristic lines vary with the local value of u and their shapes depend on the solution. Note that their slopes are infinite at the sonic line, Fig.4.10. In the lower part of the figure, a visualization of the characteristic lines was obtained fortuitously when pieces of tape were placed on the profile to cover the pressure taps.