TWO-DIMENSIONAL VORTEX

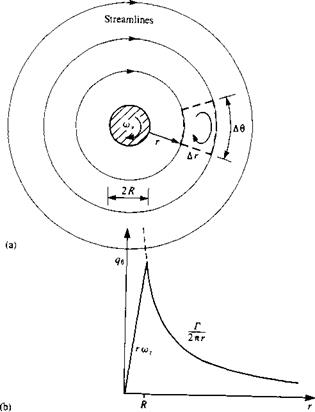
To illustrate a flowfield frequently called a two-dimensional vortex, consider a two-dimensional rigid cylinder of radius R rotating in a viscous fluid at a constant angular velocity of a>y, as shown in Fig. 2.11a. This motion results in a flow with circular streamlines and therefore the radial velocity component is zero. Consequently the continuity equation (Eq. (1.35)) in the г-в plane becomes

(2.54)

Integrating this equation results in

Чв = Чв{г)

The Navier-Stokes equation in the r direction (Eq. (1.36)), after neglecting the body force terms, becomes

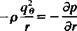(2.56)

Since qe is a function of r only, and owing to the radial symmetry of the problem the pressure must be either a function of r or a constant. Therefore, its derivative will not appear in the momentum equation in the в direction

FIGURE 2.11 Two-dimensional flowfield around a cylindrical core rotating as a rigid body.

(Eq. 1.37),
SK 1 ®l V <§!«& – її + a. II о	(2.57)
and since qe is a function of r only,
0 = d/дЛ dr2 drr)	(2.58)

Integrating with respect to r yields

dqe,4e_ n

j ‘ — Cl

dr r

where Cj is the constant of integration. Rearranging this yields

and after an additional integration
cx C2	(2.59)
q,~T’*T
The boundary conditions are
qe – —Ro)y at r = R	(2.60a)
qe~0 at r = oo	(2.606)

The second boundary condition is satisfied only if C, = 0, and by using the first boundary condition, the velocity becomes

From the vortex filament results (Eq. (2.53)), the circulation has the same sign as the vorticity, and is therefore positive in the clockwise direction. The circulation around the circle of radius r, concentric with the cylinder, is found by using Eq. (2.3)

Г = j qerdd = 2o)ynR2 (2.62)

hn

and is constant. The tangential velocity can be rewritten as

This velocity distribution is shown in Fig. 2.116 and is called vortex flow. If r-*0 then the velocity becomes very large near the core, as shown by the dashed lines.

It has been demonstrated that Г is the circulation generated by the rotating cylinder. However, to estimate the vorticity in the fluid, the integration line shown by the dashed lines in Fig. 2.11a is suggested. Integrating the velocity in a clockwise direction, and recalling that qr = 0, results in

<£ q • d = 0 • Ar + – —^ – (r + A г) Д0-0•A r – ■— г Д0 = 0 7M 2 n(r + Ar) 2 лг

This indicates that this vortex flow is irrotational everywhere, except at the core where all the vorticity is generated. When the core size approaches zero (Л—»0) then this flow is called an irrotational vortex (excluding the core point, where the velocity approaches infinity).

The three-dimensional velocity field induced by such an element is derived in the next section.