3D Vortex Sheet Strength Divergence Constraint

Although vortex sheets have many attractive properties for representing aerodynamic velocity fields, their main drawback in 3D is that the vortex sheet strength 7 is a vector whose components are not entirely independent. The complication stems from the vorticity field having identically zero divergence due to its curl definition.

V ■ ш = V-(VxV) = 0

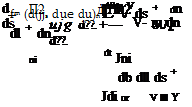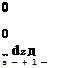Using the locally-cartesian stn sheet coordinates, the resulting divergence of a lumped vortex sheet strength 7 can then be determined by lumping the divergence of the vorticity.

The surface-gradient operator V definition simply excludes the n component. The integral J dwn/dn dn vanished since the n,n2 endpoints are assumed to be outside the vorticity layer where wn = 0.

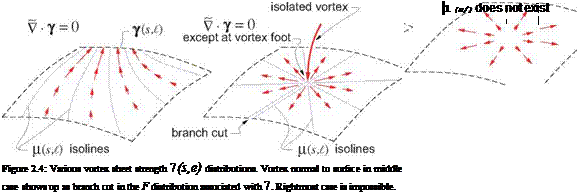Equation (2.34) is the key constraint on the 7 vector. In effect, the 7 vectors in the vortex sheet must resemble the velocity vectors in 2D incompressible flow which also have zero divergence. Figure 2.4 shows three vortex sheet strength 7(s, e) distributions. The second case has a nonzero (singular) divergence at one isolated point, which requires a vortex filament to be attached at that point normal to the surface. The third case is nonzero 7 divergence everywhere which is impossible given the vorticity-lumping assumptions.

An effective way to ensure that 7 has a zero surface-divergence is to introduce a scalar function ^(s, e), which defines 7 via f’s surface gradient, rotated 90° about the surface unit normal.

Note that any 7 defined in this manner automatically has zero surface divergence

so that (2.33) ensures that wn = 0. Conversely, if there is a point or line where concentrated vorticity is shed with wn = 0, such as along the trailing edge of a lifting wing, then f(s/) must be discontinuous on a branch cut extending from the point, as shown in Figure 2.4. Such a branch cut must be accounted for in any calculation method which seeks to determine f(s/). In a case of a lifting wing, the branch cut is typically placed all along the trailing edge from which vorticity is shed into the otherwise irrotational flow.

One conceptually useful interpretation of f(s/) is that it’s a streamfunction for 7(s, e), guaranteeing its zero divergence just like the conventional streamfunction ф(х, х) guarantees zero divergence of V(x, z) in two­dimensional flow. And just as streamlines of V follow constant-^ lines, the vortex lines parallel to 7 follow the constant-F lines on the vortex sheet, as shown in Figure 2.4.