Case Study: Transonic Compressor Rotor

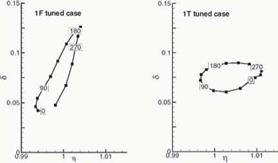
The second test case studied here is the rotor of a single stage transonic compressor rig [3], representative of a modern HP compressor front stage. It consists of 16 carbon-fiber reinforced rotor blades mounted on a titanium disk, and of 19 stator vanes. The tip diameter is 0.38m, maximum relative rotor in­let Mach numbers reach Ma = 1.4 at the tip. At the design speed of 10,000 RPM, the FEM analysis yields the frequencies of 161 Hz for the 1F eigenmode, and 1505 Hz for the 1T eigenmode. The aerodynamic inflience coefficients for the rotor were calculated for these two modes, and the aeroelastic eigenvalues were deduced from Eq. 6, assuming a constant mechanical damping (logarith­mic decrement) for each mode of 5mech = 0.01. The results for a perfectly tuned case are shown in Fig. 6, with the 1F-related eigenvalues on the left, and the 1T related ones on the right hand side. The eigenvalues are shown as damping (log. dec.) over frequency ratio n = f/f0 with f0 being the in-vacu eigenfrequency of the respective modes. For the tuned cascade, the eigenvec­tors are the well known traveling wave modes with constant interblade phase angle, which is indicated by the inset labels in Fig. 6. The results show that the cascade is aeroelastically stable, all damping values are greater than zero. The damping is in all cases significantly larger than the mechanical damping of 5mech = 0.01, indicating that the vibrational behavior of the cascade is dom­inated by the aerodynamic damping and coupling. Finally, Fig. 6 shows that

the eigenfrequencies of the cascade differ up to approximately 1% from the in-vacuo eigenfrequency due to the unsteady aerodynamic forces.

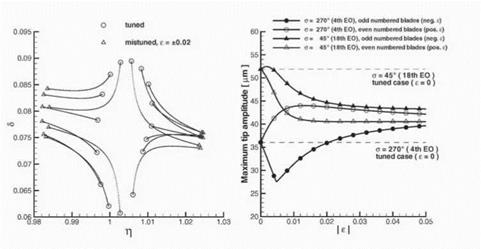
In the following, the effects of frequency mistuning are studied on the 1T eigenmode. First, alternating frequency mistuning is introduced, i. e. the gener­alized stiffnesses are decreased for the odd numbered blades and increased for the even numbered ones. Figure 7 shows the aeroelastic eigenvalues for the 1T mode. The circles correspond to the tuned configuration, while the triangles denote the mistuned configuration with a mistuning parameter of є = ±0.02. Furthermore, the trajectories of the eigenvalues for the values between є = 0 and є = ±0.02 are indicated by the lines. The results show that the damp­ing values converge towards the mean of the tuned configuration values, so that the damping of the least stable eigenvalue is increased, i. e. the cascade is aeroelastically more stable. The alternating mistuning separates the eigen­values into two distinct clusters, each forming a small ovoid similar to the one of the tuned configuration. This indicates that the blades of equal in-vacuo resonant frequencies are coupled through the unsteady aerodynamic infhence coefficients spanning two blade passages, while the immediate neighbors are increasingly decoupled from one another due to their differing structural pa­rameters. When using the same mistuning pattern and applying external exci­tation forces, the resonant amplitudes arise as shown in Fig. 8. In this figure, the triangles show the situation for a four engine order (EO) excitation, the circles denote the response amplitudes for an 18 EO excitation, while open and solid symbols denote the response of the odd and even numbered blades, respectively. A first observation from this plot is that the responses for the tuned configuration strongly depend on the EO of the excitation – which is due to the difference in aerodynamic damping, as found in Fig. 6. Furthermore, the resonant responses for the 18 EO excitation decrease with increasing al­ternating mistuning, while those for the 4 EO excitation increase, at least for

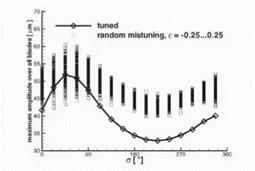
the even numbered blades, which show the higher amplitudes. This result im­plies that, in certain cases, deterministic mistuning can be used to decrease the response amplitudes in comparison to the tuned configuration. Finally, the in- flience of random mistuning on the resonant response has been studied. 500 cases of randomly generated frequency distributions with the mistuning rang­ing from є = 0 to є = ±0.25 have been generated and analyzed for excitation EOs between 0 and 16, corresponding to interblade phase angles of a = 0° to a = 360°. In Fig. 9, the resulting maximum response amplitudes are plotted. The figure shows that for excitation interblade phase angles of a > 90°, all

randomly selected distributions result in larger maximum amplitudes than for the tuned case, while for a = 0° to a = 90°, some configurations exist with resulting maximum amplitudes that are lower than for the tuned configuration. The majority of the configurations nevertheless yield higher amplitudes than in the tuned case, and in the worst mistuned case, exceeding the tuned amplitude by more than 40%. It can be observed that the largest relative increase occurs for the excitation interblade phase angle with small tuned response amplitudes and that the spread of the resulting mistuned maximum amplitudes corresponds to the tuned amplitudes for each excitation interblade phase angle: It is small for the cases with small tuned amplitude, and large for cases with large tuned amplitudes. Given the fact that the actual configuration of the stochastic mis – tuning in a real machine cannot be controlled or predicted, it is obvious that the predictions from a tuned cascade model do not yield a conservative value for the resulting maximum amplitudes, but generally produce too low values.

4. Summary and Conclusions

A numerical method has been presented that can be used to study the effects of structural mistuning on the aeroelastic behavior of turbomachinery cascades. The method has been validated using data from a recent high pressure turbine experiment and has proven to yield acceptable results in describing the magni­tude and distribution of mistuned resonant response amplitudes on the turbine rotor blades. Further case studies on the same turbine rig and on a transonic compressor rig rotor have been performed to demonstrate the multitude of phe­nomena that can be observed in mistuned aeroelastic systems.

The method presented here has been successfully applied to the modeling of some of these phenomena. Owing to its formulation with only a few degrees – of-freedom, it is very fast and thus well suited to perform parametric variations or stochastic "Monte-Carlo" – simulations.