DESIGN OF THE Нж AUTOPILOT

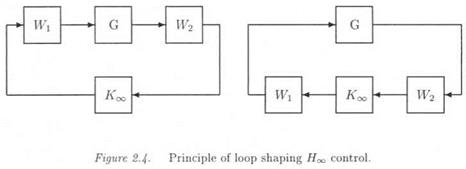
1.1.1 PRINCIPLE OF LOOP SHAPING Нж CONTROL

In the case of a SISO system, the very classical Bode method shapes the magnitude and phase ofthe open loop frequency response K(jut)G(ju>), where K(s) and G(s) respectively represent the controller and plant model. As an extension to the case of a MIMO plant 0(5), the sin­gular values of the open loop transfer К (jut ) G )К ) or G (juj ) К (К ( can be shaped (McFarlane and Glover, 1990; McFarlane and Glover, 1992). To this aim, pre – and post-compensators IEi(s) and W2G) are added at the plant inputs and outputs. These transfer matrices Wi(s) are chosen so that the singular values сг; ( К Gg)G(К) К )К) ) reflect the design objectives.

A specific robust stabilization procedure is then applied to the aug­mented plant W2GW1 (see Figure 2.4). A controller Ко is obtained, which stabilizes the augmented plant. The final controller is K(s) = ITrx(s)-K’oo(s)W2(s). Note that the above robust stabilization procedure presents special properties, since it tries as much as possible to keep the desired open loop shaping while enforcing a stability closed loop con­straint.