Equivalence of Vortex and Doublet Sheets

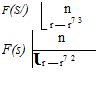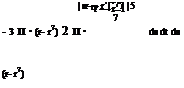The vorticity streamfunction f(sY) can also be interpreted as the normal-doublet sheet strength. An area element ds dt of the doublet sheet in effect has an infinitesimal 3D doublet of strength dKn = f ds dt, oriented along the normal direction. In two dimensions, the element ds of the sheet has an infinitesimal 2D doublet of strength dKn = f ds. The resulting velocity fields in 3D and 2D are

which are the same as the VY(r) fields of the equivalent vortex sheets given by (2.16) and (2.24). This equivalence can be verified with some effort by substituting 7 = n xVp into (2.16) or (2.24) and integrating by parts.

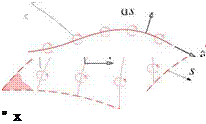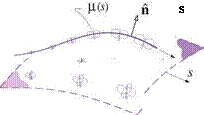
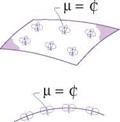
Figure 2.5 illustrates the doublet-sheet/vortex-sheet equivalence for 3D and 2D sheets. In general, a linearly – increasing p is equivalent to a constant-magnitude 7, and vice versa. At the edge of the doublet sheet, p(s, e) in effect has a step change to zero. Here Vp and the corresponding 7 have an impulse, which is equivalent to a vortex filament of strength Г = p along the sheet edge. Figure 2.6 shows the constant-strength doublet sheet case.

Figure 2.5: Equivalence between normal-doublet sheet and vortex sheet away from edges, for 3D and 2D cases. The doublet and vortex sheets have the same velocity fields.

Figure 2.6: Constant-strength normal-doublet sheet with edges, and the equivalent vortex filaments, for 3D and 2D cases.

Because the elimination of the zero-divergence requirement for 3D vorticity is such a great simplification, doublet sheets are heavily favored over vortex sheets in all common 3D panel methods. However, the zero – divergence constraint does not appear in 2D, with the result that vortex sheets tend to be favored over doublet sheets in 2D panel methods. For an extensive review and implementation details of various 2D and 3D panel methods see Katz and Plotkin [4].

In the subsequent discussions and applications here, we will employ either vortex or doublet sheets as most appropriate. In particular, constant-strength doublet panels which are equivalent to vortex rings will be used for 3D configuration analyses in Chapters 5 and 6.