Forces and Moment

The nonlinearity of the governing equation does not allow for superposition of ele­mentary solutions nor the decomposition of the problem into a symmetric and lifting problems. However, the symmetric problem still has zero lift and moment, but wave drag may occur when supersonic regions are present in the flow.

The lift is given by the integral seen earlier

Q = j (c~p (x) — C+ (x)) ddx = J {2u+(x) — 2u — (x)) ddx =

This result is consistent with the Kutta-Joukowski lift theorem. The drag is also calculated as before

One can substitute the following expressions from the tangency conditions

Another approach to evaluating the drag is based on the x-momentum theorem applied to a control volume with exterior unit normal, whose boundary Sfi is made of a large circle of radius R, connected by a cut C to the profile P and shock(s) Sk that are excluded, see Fig.4.13. Inside the domain bounded by Sfi, the flow is smooth. Application of the divergence theorem to the x-momentum Euler equation leads to the contour integral

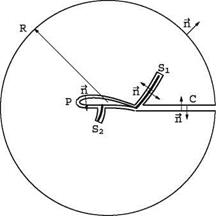Fig. 4.13 Contour for evaluation of the drag integral

On the circle R, the perturbation velocity (u, w) decays as R resulting in

no contribution. Along the profile P the contribution is precisely the drag force D’. Along the cut C the flow is continuous and again no contribution will occur, but along the shock(s) Sk the flow is discontinuous. For the full Euler equations, though, there would be no net result from the shocks, because the jump conditions would be satisfied there and more precisely

< p(V. Vt) >= 0, < pU(1 + u)(VV) + pnx >= 0 (4.97)

from conservation of mass and x-momentum. This is no longer true when the solution is approximated by its leading terms (u(1),w(1)). The only two non zero contributions are therefore along the profile and along the shock(s).

4

Mass and momentum are conserved to second order (O (e 3)), but to third order this is no longer the case. Indeed, expanding the conservation of mass and x-momentum to third order gives

e2 {!(Ku(2) + p(3) + u(1)p(2) + p(1)u(2)) + !(w(2) + p(1)w(1))} = 0 e2 {! (Ku(2) + p(3) + 2u(3) + p(3) + 2u(1)p(2) +

2p(1)u(2) + 2u (1)u(2) + p(1)u(1) 2)

+ д (w(2) + p(1)w(1) + u (1)w(1))} = 0

(4.98)

Subtracting the first equation from the second yields a combined mass-momentum equation

_(u(3) + p(3) + u(1)p(2) + p(1)u(2) + 2u(1)u(2) + p(1)u(1) 2)

Upon replacing p(1) and p(2) from previous results, this reduces to

The last term in the ^-derivative is of higher order and can be removed, while the

This equation is equivalent to the previously derived governing equation for smooth flow, since it can be written as

However, when the flow is discontinuous, such as at a shock, the solution (u(1), w(1)) to the low order governing equations does not satisfy the jump conditions associated with this new conservation equation. In fact, the mass and x-momentum are not conserved at third order. This is consistent with the fact that the flow is irrota – tional to the first two orders but not to third order. Hence drag appears at third order (O (e2)). If we revert to the physical variables, the drag reads

D = pU2 < (1 – m0) – Y + m+ 3 – nx + uw nz > dl (4.106)

Jsk 23 2

where Sk represents the shock line(s) with arc length l and + is the normal unit vector to Sk oriented in the flow direction. This determines how the jump is calculated, i. e. downstream values minus upstream ones. Here we have used the combined mass – momentum equation. The reason for using this equation is that mass is not conserved
to third order, therefore, this imbalance will add momentum in the flow direction in the amount corresponding to < pU(V. it) > which must be subtracted from the x-momentum given by < pU(1 + u)( V. it) + pnx >.

The above expression for D’ can be simplified further by using the shock con­ditions derived earlier. As a first step, one eliminates the nz component from the irrotationality condition

< w >

nz = nx (4.107)

<u>

we also make use of the identities < a2 >= 2a < a > where a = a1+a2 is the average value across the discontinuity, < ab >= a < b > +b < a > and < a3 >= (a2 + 2a2) < a >. The jump term in D’ now reads

The final step consists in using the shock polar relation multiplied by <— nx and subtract it from the above equation

One finds the following result

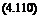
Y + 1 2 2 2_ 2

M2(u2 + 2u ) < u > + (y + 1)M^u < u >

This can be rearranged to read

— YITM2 < u >3 nx (4.111)

The drag is thus

D = — MlpU2 < u >3 nxdl

12 Jsk

or the drag coefficient

Y + 1 2 3 dl

Cd — – м2 < u >3 nx— (4.112)

6 4 c

This makes it clear that if there are no shock waves in the flow, the wave drag is zero.

The moment is obtained from

M, o = – pU2 ^ xdx

and the moment coefficient