Geometric Similarity

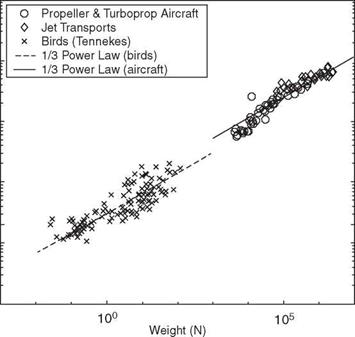
The concept of geometric similarity can help relate different physical quantities by means of the dimensional argument. Under the assumption of geometric similarity, Figure 1.20 correlates wing loading with the weight of a vehicle. For example, the wing loading is proportional to the one-third power of the weight as shown later, if the aerodynamic parameters remain unchanged (which is not true, as is discussed in detail). If flyers are assumed to be geometrically similar, the weight W, lift L, and mass m for unaccelerated level flight, can be expressed with respect to a characteristic length l (e. g., chord length (c), mean chord length (cm), or wing length (R)) as

W = L = mg. (1-3)

The wing area and flyer’s weight are expressed as

S – l2, W – l3. (1-4)

Then the wing loading can also be expressed as

W = kxW1/3, (1-5)

where k1 is a constant to be determined empirically. Liu [57] shows that a suitable value of k1 is 53 and 30.6 for aircraft and birds, respectively. The correlation is shown in Figure 1.20.

2 Wingspan

When studying flapping animals, parameters of interest are often related to the body mass m of the animal. Using the dimensional argument method and assum­ing geometric similarity for the animals considered, one can determine a relation between the wingspan and mass. Collecting data from Tennekes [29] for birds rang­ing from a 0.026-N black-chinned hummingbird to a 116-N mute swan, and data for propeller/turboprop aircraft and jet transports published by Jackson [58] covering a broad spectrum of aircraft from a 1500-N ultralight to a 1800-kN Boeing 747-400, Liu [57] suggests that, over a large range of the weight, birds and aircraft basically follow the power law:

l = 1.654m1/3 (aircraft); l = 1.704m1/3 (birds). (1-6)