Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Hysical Properties of the Atmosphere
Changes of pressure, density, and viscosity of the air with altitude z of the stationary atmosphere are important for aeronautics. These quantities depend on the vertical temperature distribution T(z) in the atmosphere. At moderate altitude (up to about 10 km), the temperature decreases with increasing altitude, the temperature gradient dT/dz varying between approximately—0.5 and —1 К per 100 m, depending on the weather conditions. At the higher altitudes, the temperature gradient varies strongly with altitude, with both positive and negative values occurring.
The data for the atmosphere given below are valid up to the boundary of the homosphere at an altitude of about 90 km. Here the gravitational acceleration is already markedly smaller than at sea level.
The pressure change for a step of vertical height dz is, after the basic hydrostatic equation,
dp = —ggdz
ego d-H
where H is called scale height.
|
Table 1-1 Density q, dynamic viscosity /і, and kinematic viscosity v of air versus temperature t at constant pressure p « 1 atmosphere
|
|
The decrease in the gravitational acceleration g(z) with increasing height z is
|
|
Table 1-2 Reference values at the atmosphere layer boundaries, T
* After “U. S. Standard Atmosphere” [2]. Zfj, Tfr values at the lower boundary of the layer height; dTjdH, n values in the layers. |
which shows that each polytropic exponent n belongs to a specific temperature gradient dT/dH. Note that the gas constant[1] in the homosphere, up to an altitude of H = 90 km, can be taken as a constant.
From Eq. (1-13) follows by integration:
T = T„ – (H – H„) (1-14)
Here it has been assumed that the polytropic exponent and, therefore, the temperature gradient are constant within a layer. The index b designates the values at the lower boundary of the layer. In Table 1-2 the values of Hb, zb, Tb, and dT/dH are listed according to the “U. S. Standard Atmosphere” [2].
 |
 |
 |
 |
||
The pressure distribution with altitude of the atmosphere is obtained through integration of Eq. (1-12д) with the help of Eq. (1-14). We have
 |
 |
 |
 |
For the special case n = 1 (isothermal atmosphere), Eq. (1-15д) reduces to
In the older literature this relationship is called the barometric height equation. Finally, the density distribution is easily found from the polytropic relation Eq. (1 -11*)-
Also given in Table 1-2 are the reference values pb and ob at the layer boundaries. For the bottom layer, which reaches from sea level to H~ 11 km, Hb = H0 has to be set equal to zero in Eqs. (1-15a) and (1-15£>). The other sea level values (index 0), inclusive of those for the speed of sound and the kinematic viscosity, are, after [2],
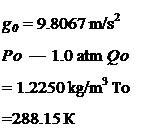t0 = 15°C a0 = 340.29 m/s vQ = 1.4607 • 10’5 m2/s (dT/dH)о = -6.5 K/km
|
Table 1-3 Barometric pressure p, air density q, temperature T, speed of sound a, and kinematic viscosity v versus height z*
* After “U. S. Standard Atmosphere” [2]. |
The numerical values of pressure and density distribution are listed in Table 1*3, to which the values for the speed of sound and the kinematic viscosity have been added. More detailed and more accurate values are found in the comprehensive tables [2].
Finally, in Fig. 1-2, a graphic representation is given of the distributions of pressure, density, temperature, speed of sound, and kinematic viscosity versus altitude. Whereas pressure and density decrease strongly with height, kinematic viscosity increases markedly.
