Integral Velocity / Vorticity-Source Relations

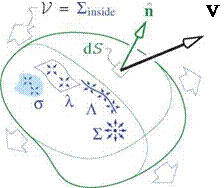
Consider the volume flow rate V outward through a closed surface, defined as the area integral of the normal velocity component over the surface, as shown in Figure 2.7 on the left.

The second form in (2.39) follows from Gauss’s theorem, for which the volume integral is evaluated over the volume inside the surface. The alternative forms in (2.40) follow from the source density definition (2.1) and the various lumped source sheet, line, and point definitions, and are evaluated over all the source singularities present inside the volume bounded by the surface. The overall result is that V for a closed surface is equal to the sum of all the point sources or integrated volume, sheet, or line source distributions inside.

Figure 2.7: Volume outflow V through closed surface (left) is equal to the total integrated source strength of all source density, sheets, filaments, and points inside. Circulation Г over closed circuit (right) is equal to the total circulation of all vorticity, vortex sheets, and vortex filaments enclosed or encircled by the circuit.

Next consider the circulation Г about a closed circuit, defined as the line integral of the tangential velocity component around the circuit, indicated in Figure 2.7 on the right.

Г = V ■ dl = (VxV) ■ A dS

enclosed

= Ш ■ A dS + Y ■ Ads + Г = Tendosed

enclosed enclosed

The second form in (2.41) follows from Stokes’s theorem, for which the area integral is understood to be evaluated over any surface bounded by the contour, with A being the unit normal on this surface. The alternative forms in (2.42) follow from the vorticity definition (2.2) and the various lumped vortex sheet and line definitions. The overall result is that the circuit circulation Г is equal to the total strength of all the integrated vorticity, vortex sheets, and vortex filaments enclosed by the circuit. Any vortices outside the circuit have no contribution to Г.