Mathematical Model Building

2.1 INTRODUCTION

An aircraft can be considered as a dynamic system while in any type of dynamic- flight operation, since flight-related control functions to be performed are necessarily (1) the deflection of (aerodynamic) control surfaces and (2) the change in the engine thrust, which acts as input to the dynamic system, and the responses of the aircraft are the desired outputs: an equilibrium state of the aircraft’s motion, stabilized aircraft motion after a disturbance, and a change of one equilibrium state to another, if required. An aircraft is made of structures/materials, and has to have an engine for providing thrust, avionics systems, and control mechanisms; moreover, it has to ultimately fly in the air and the above-mentioned operations are called upon to be performed for any successful flight mission. Hence, the subject of flight mechanics can be and should be studied from the ‘‘control system’’ point of view. This study involves modeling and analysis of the dynamic system (in general, an atmospheric vehicle).

A study of the dynamic system can be performed via analytical or experimental means. The analytical approach yields a mathematical model based on several assumptions (because real-life dynamic systems are mostly/often nonlinear and distributed in nature) and application of the theory and concepts of modeling. In an experimental approach one has to design an appropriate experiment and generate data for analysis. This analysis is mainly carried out by using signal processing, system identification, and parameter-estimation techniques. Mathematical modeling of dynamic systems is very essential for analysis, design and simulation of control systems, and for prediction of behavior of these systems. A mathematical model characterizes the static and dynamic behavior of a system. Some practical examples are use of mathematical models in flight simulation and design of control systems for aerospace vehicles (like aircraft, rotorcraft, missile, unmanned aerial vehicles, micro­air vehicles, and spacecraft), weather forecasting, control of robotic systems, use in optimization of chemical processes in industries, and analysis of communications and biomedical signals.

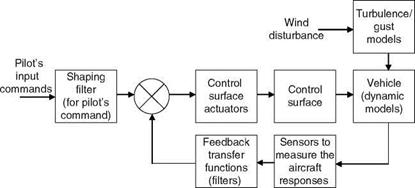
A system is a set of components or functional activities that interact with each other to complete a specified task or a mission. Some examples of systems are chemical plants, robotic systems, atmospheric vehicles, computer networks, and the economy (process) of a country. Most dynamic systems are described by differential/difference equations. There is exchange or change of energy and dissi­pation in (damped) systems. A real-life dynamic system can be modeled using a mathematical model, which should be obtained, refined, and validated based on the acquired/actual data from the experiments on the system. The choice of a gross model is dictated by previous experience and the physics of the problem at hand. A fair amount of knowledge is generally accessible to the model developer/analyst. A system, in general, consists of a collection of variables needed to describe its dynamic behavior at some point in time. A system could be continuous-time or discrete-time when the state variables change either continuously or at discrete points in time (in sampled data systems), respectively. In aerospace applications, mixed – type models are used (Chapter 9). A typical atmospheric vehicle (control) system is shown in Figure 2.1. The terms system, plant, and process are used interchangeably. An aircraft can be called a system, whereas a chemical system is called a plant. This plant involves various processes for which again some mathematical models are required. A telephone/computer network can also be called a system. In many problems in science and engineering, one finds a crucial need to represent a dynamic system by its mathematical model.

This model is used for a variety of reasons: (1) to study basic dynamic charac­teristics of the system, (2) to predict future behavior of the system, e. g., weather forecasting, (3) to analyze the stability and control characteristics of the system so as to help monitor, modify, regulate, or control the behavior of the dynamic process/plant/system, e. g., chemical reactors, (4) to simulate the responses of the system for various kinds of inputs/environment, e. g., flight dynamics simulator (Chapter 6), and (5) to optimize cost and to reduce losses, e. g., dynamics of the economy of a country.

Thus, mathematical models are used in research for interpretation of acquired knowledge or measurements that provide clues for further investigations [1]; e. g., first a simplified model of the system is used and then, based on the analysis of experimental data, this model is revised. A mathematical model for the purpose of designing a new system or a controller for the same system is expressed in a manner that is compatible with the design criteria: guaranteeing the basic static/dynamic stability, overall performance, tracking error minimization, safety, and cost. For example, a time-domain model will be more suitable for use in

control-optimization methods based on time-domain methods and hence the know­ledge of components and subsystems should be in such usable forms. Finally, the control actions on a system depend on the knowledge about the system.

A mathematical model is a simplified representation of a system that helps in understanding, predicting, and possibly controlling the behavior of the system [1,2]. A model presents the knowledge about the system in a very practical form. In fact a model simulates or mimics the behavior of the system. Models could be of several types: hardware models (like the scaled model of an aircraft, a missile, or a spacecraft that is used in wind-tunnel testing), software expressions/computer algorithms, conceptual or phenomenological, physical, and symbolic models like maps, graphs, and pictures. A model represents a reality, the system, phenomenon, or process under study, with reduced complexity. Scientists and engineers all over the world make major efforts to understand the various natural phenomena as well as the properties and characteristics of man-made systems. Mathematical modeling is one of the most fascinating and intriguing fields of research. It encompasses the study of determin­istic and stochastic systems. Stochastic systems are, in general, difficult to model. Hence, a midway approach is usually preferred: deterministic systems affected by additive or multiplicative random noise.

There are three basic reasons why the usual deterministic systems/control theories do not provide a complete means of performing this analysis and design [3]:

(a) No mathematical model of a given system is perfect. Effects are modeled approximately using a mathematical model. There are many sources of uncertainty in any mathematical model of a system. Certain types of uncertainties can often be described by some random phenomena. Some uncertainties can be described by bounded but unknown disturbances that are nonrandom in nature. Between-the-events uncertainties can be axiomatically defined by probability theory, which is fundamentally based on binary or crisp logic. Within-the-events uncertainties can be modeled using the concepts of fuzzy logic (FL), which is a multivalued logic.

(b) Dynamic systems are driven not only by deterministic control inputs but also by disturbances that are neither controllable nor deterministic. Such disturbances are random and are usually modeled by the white Gaussian process. However, non-Gaussian, uniform, or other kinds of noise processes are sometimes present. Atmospheric turbulence and gust act on a flying vehicle.

(c) Measurements (sensors) do not provide perfect and complete data about a system. They introduce their own system dynamics and distortions. They are also corrupted with noise.

In the light of the above observations, the following questions become very relevant and interesting [3]: (1) What kind of models should be used to explain such uncertainties, for example, Gaussian or uniform probability distributions, or bounded disturbance models? (2) With such noisy data, how do we use the system models to optimally estimate the quantities of interest to us? System identification, state estimation, and specifically parameter estimation [4] and estimation of the spectra
of signals play an important role in analysis. (3) How do we control the system’s behavior in the face of these uncertainties, e. g., design of a suitable optimal control­ler? (4) How do we evaluate the performance of such estimators and control, for example, quality or goodness-of-fit criteria, stability (gain and phase) margins, error performance, and robustness of performance?

Some of the foregoing aspects are studied in the context of flight mechanics modeling and analysis in this book. A two-way approach to mathematical modeling is illustrated in Figure 2.2 [1]. The left side depicts the analytical route for model building and the right side the empirical data-based model-building route. The block diagram illustrates the comprehensive process of building a mathematical model. Most systems are nonlinear and distributed in nature: there are two independent variables—time and space. Such systems are called distributed systems and can be described by partial differential equations (PDEs). When the linearization process is accomplished, linearizing errors will occur because of approximation. If the spatial effects are lumped, then we get linear models described by ordinary differential equations (ODEs). Such systems/models are called lumped systems. At this stage we obtain a model that can be postulated for further analysis and revised based on the systematic application of the right side path. The measured data are used in system identification/parameter-estimation procedures to arrive at an adequate model struc­ture and parameters of the mathematical model [4]. This path involves measurement noise, data handling errors, quantization errors, and estimation errors.

FIGURE 2.2 A two-way approach to mathematical model building.