Moving Coordinate System

The linearized equations which are obtained previously enable us to analyze aerodynamical problems more conveniently. Let us now elaborate on the coor­dinate systems which will further simplify the equations. The type of external flows we study usually considers a constant free stream velocity U at the far field. The reference frame used for this type analysis is a body fixed coordinate system which moves in the negative x direction with velocity U. Another type of analysis is based on the moving reference system which moves with the free stream. With this type analysis, the form of the equations looks simpler to handle. Let us write Eq. 2.24b in the moving coordinate system which moves with the free stream. Let x, y, z be the body fixed coordinate system and, x0, y’, z’ be the flow fixed coor­dinate system. As seen from Fig. 2.3, since the free stream velocity is U, after the time interval t the flow fixed coordinate system translates in x direction by an amount Ut.

The relation between the two coordinate system reads as x = x — Ut, y = y, z = z, t = t.

The derivative with respect to t0 becomes

0 0 0 0x 0 0

0t’ 0t ^ 0x’ 0t 0t ^ 0x’ U.

Here, %= -U.

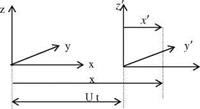Fig. 2.3 Body fixed x, y, z and the flow fixed x’, y’, z’ coordinate systems

The partial derivatives with respect to body fixed coordinates in terms of the flow fixed coordinates then become:

0 _o__o _0-A _0-A _0-A

0t ^ 0x 0t’ 0x 0x’ 0y 0y’ 0z dz’ Equation 2.24b in the flow fixed coordinate system reads as

The last equation is in the form of the classical wave equation whose solutions are well known in mathematical physics. The boundary conditions and the pres­sure coefficient expressions, Eqs. 2.20 and 2.21, become:

Boundary condition: w

Pressure coefficient: Cp

2.1.5.1 Summary

Hitherto, we have given the linearized form of the potential equations which are applicable to various problems of classical aerodynamics. In order for these equations to be valid in our modeling, the following assumptions must be true:

1. The air is considered as a perfect gas.

2. Mass, momentum and the energy conservations are used.

3. Body forces, viscous forces and the chemical reactions are ignored.

4. The flowfield is assumed to be either incompressible or barotropic.

5. The slopes of the body surfaces and all the flowfield perturbations are assumed to be small.

6. The time rate of change of the flow parameters are assumed to be small.

In addition, the linearized form of the compressible flow is only valid for subsonic and supersonic flows. The nonlinear approaches for the transonic and the hypersonic flows will be seen separately in relevant chapters.