POSITION, VELOCITY, AND ACCELERATION OF THE VEHICLE MASS CENTER

POSITION AND VELOCITY RELATIVE TO THE EARTH

The location of the vehicle mass center relative to Earth is given by the spherical polar coordinates ЗІ (geocentric radius), ц (longitude), and X (latitude). Their rates of change are related to the Fv components of velocity relative to Earth by (see Fig. 5.2)

Я = – Vе.

ZT

u —___ 1__ Vе

* Зі cos X y*

A = —

The components of E are in turn given by [see (4.2,1)]

YEy = I‘vw(^w = – ЦтвСУв "Ь Wв) (5.3,2)

where

	~V		1__
Yw —	0	; Ww =	W n Vw
	_0_		w Lrr zwJ
	~u
Yb =	V	; WB =	K
	w_		Wz.

and ¥ is the airspeed of the vehicle, i. e. its speed relative to the atmosphere. When the atmosphere is at rest relative to Earth, W = 0 and (5.3,2), (5.3,3), and (4.5,4) yield

VеXp = V cos 0W cos y>w

VEyy = V cos 6W sin y>w (5.3,4)

VEZp = —V sin 6W

Substitution of (5.3,4) into (5.3,1) provides the polar coordinates in the

130 Dynamics of atmospheric flight more convenient forms

0t = V sin ew
V

ft = — cos dw sin %pw sec A (6.3,5)

Я = — cos 0W cos y>w

Using the body-axis velocity components an alternative system of equations

is

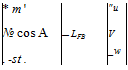(5.3,6)

When the motion considered takes place over only a small portion of the Earth’s surface, the latter may be regarded as locally flat, and the vehicle position is then more conveniently referenced to a frame Fe located in its immediate vicinity—for example, at the initial point of the trajectory. In this case Fv may be assumed parallel to Fe, and the position coordinates of the mass center (xE, yE, zE) are governed by the differential equations

xE = V cos 6W cos y>w

yE = V cos Ojfr sin iffy (5.3,7)

iE = — V sin 6W