Rates of strain, rotational flow and vorticity

As they stand, the momentum Eqns (2.66) (or 2.67), together with the continuity Eqn (2.46) (or 2.47) cannot be solved, even in principle, for the flow velocity and pressure. Before this is possible it is necessary to link the viscous stresses to the velocity field through a constitutive equation. Air, and all other homogeneous gases and liquids, are closely approximated by the Newtonian fluid model. This means that the viscous stress is proportional to the rate of strain. Below we consider the distortion experi­enced by an infinitesimal fluid element as it travels through the flow field. In this way we can derive the rate of strain in terms of velocity gradients. The important flow properties, vorticity and circulation will also emerge as part of this process.

2.7.1 Distortion of fluid element in flow field

Figure 2.24 shows how a fluid element is transformed as it moves through a flow field. In general the transformation comprises the following operations:

(i) Translation – movement from one position to another.

(ii) DilationjCompression – the shape remains invariant, but volume reduces or increases. For incompressible flow the volume remains invariant from one position to another.

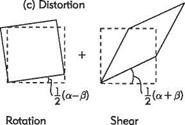
(iii) Distortion – change of shape keeping the volume invariant.

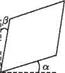
Distortion can be decomposed into anticlockwise rotation through angle

(a — 0)/2 and a shear of angle (a + /?)/2.

The angles a and (3 are the shear strains.

Fig. 2.24 Transformation of a fluid element as it moves through the flow field