THE BIOT-SAVART LAW

At this point we have an incompressible fluid for which the continuity equation is

V • q = 0 (1.23)

and where vorticity £ can exist and the problem is to determine the velocity field as a result of a known vorticity distribution. We may express the velocity field as the curl of a vector field B, such that

q = V X В (2.64)

Since the curl of a gradient vector is zero, В is indeterminate to within the gradient of a scalar function of position and time, and В can be selected such that

V-B = 0

The vorticity then becomes

% = V X q = V X (V X B) = V(V • B) – V2B

By applying Eq. (2.65) this reduces to Poisson’s equation for the vector potential B:

$=-V2B (2.66)

The solution of this equation, using Green’s theorem (see Karamcheti,15 p. 533) is

4л Jv |r0 —fi|

Here В is evaluated at point P (which is a distance r0 from the origin, shown in Fig. 2.12) and is a result of integrating the vorticity £ (at point r,) within the

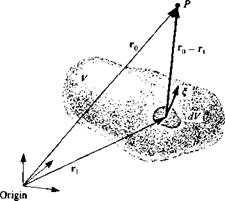FIGURE 2.12

Velocity at point P due to a vortex distribution.

volume V. The velocity field is then the curl of В

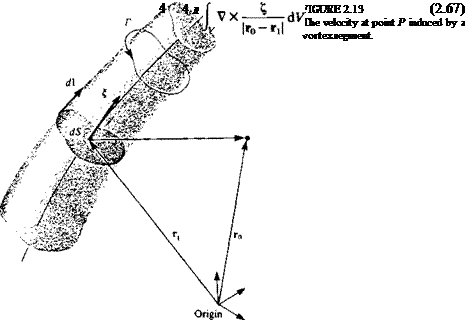
Before proceeding with this integration, let us consider an infinitesimal piece of the vorticity filament £, as shown in Fig. 2.13. The cross section area dS is selected such that it is normal to ^ and the direction d on the filament is

Also the circulation Г is

Г = £dS

and

dV = dS dl

so that

V X -—-—- dV = V X Г ——-

and carrying out the curl operation while keeping r, and d fixed we get

rrvr dl _rdl*(rO~ri)

VXr|ro-r1|-r |r0-r,|3

Substitution of this result back into Eq. (2.67) results in the Biot-Savart law, which states

Г Г dіх(г0-гі) 4л J |r0-rt|3

or in differential form

_ Г dl X (r0 – rt) 4л |г0-Гі|3

A similar manipulation of Eq. (2.67) leads to the following result for the velocity due to a volume distribution of vorticity:

-Lf txfrb-r,)^ 4л Jy |r0-r,|3

(2.67a)

q