THE DIRECTION COSINE RATES

When the direction cosines of the moving frame are used instead of the Euler angles to define its orientation relative to Fv, then the differential equations needed follow directly from (4.6,7). Let ^BF = [iw] (the same treatment holds for Then from (4.6,7)

(5.2,11)

These constitute nine differential equations for the nine l(j. Actually only three of the nine are independent (a rigid body has only three rotational degrees of freedom), and the additional six equations provided by (4.4,8) reduce the number of independent l{j to three. In the force equations given later, the direction cosines that would replace the Euler angle terms are those for the angles between the moving axes of Fw and zv, i. e. (with now denoting components of L(</(,) l13, l23, and l33. The differential equations for these are, from (5.2,11),

Ьз — Ш33 QI33

tu = – Rl13 + Pl33 (5.2,11a)

І3З = Ql 13 R^23

and for some problems only these three direction cosines are needed. Whether

direction cosines or Euler angles are preferable in any particular application depends on the situation, and on the kind of computing machinery to be used.

THE AERODYNAMIC ANGLE RATES

We shall find it convenient later to have the angular velocity of FB relative to Fw expressed in terms of the derivatives of the aerodynamic angles.

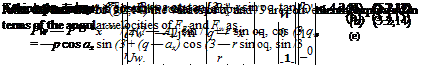
Let jB and 1%, be unit vectors in the directions of GyB and Czw, respectively. Then it follows from the definitions of oq. and /3 (Sec. 4.3) [and an argument like that for (5.2,3)] that the angular velocity of FB relative to Fw is

The group of three equations actually wanted subsequently is (5.2,14a) and (5.2,15).

Since (5.2,12) may alternatively be written

it follows that (5.2,13) through (5.2,15) apply equally when the angular velocities of FB and Fw are relative to Fv instead of FI. Then the lower-case (p, q, r) are replaced in them by (P, Q, E).