The Energy Equation in Control-Volume Form

The energy equation represents the fifth of the required six equations needed for the solution of the basic aerodynamics problem defined in the chapter introduc­tion. Specifically, it must be included in any consideration of compressible flow. The energy equation in aerodynamics is a statement of the First Law of Thermo­dynamics. The rate form of the First Law already was reduced to control-volume form in Eq. 3.22. Thus, for conservation of energy, we require that:

dr=f 0№ + Яe i-V =Q-W, (3-39)

where Q and W are the rates of heat flow and work flow from the surroundings. Only a brief discussion of the energy equation is needed here because most aspects are covered in the basic physics or thermodynamics already studied. Emphasis is on the forms needed and the notation used in compressible-flow aerodynamics.

As shown in Eq. 3.32, the rate of change of the total energy of the system of particles (expressed in control-volume form) consists of two terms: (1) the rate of change of the energy contained instantaneously within the control volume, and (2) the passage of energy through the surface of the control volume by convection with the flow.

The intensive energy variable e’, shown in the integrals in Eq. 3.39, is used to represent all forms of energy that might be resident in the fluid. It consists of several parts that must be distinguished in solving compressible-flow problems. Any differ­ential mass element in the control volume simultaneously may carry kinetic energy due to both the random motion of the molecules that comprise the element and the organized motion of the fluid. In general, there also may be potential energy due to the changing position in a body-force field (we use a uniform gravity field to illus­trate). Thus, the energy, e’, per unit mass often is defined in fluid-mechanics problems to consist of the following three terms:

V 2

e’ = e + — + gz, (3.40)

where e is defined as the internal kinetic energy (due to random microscopic mol­ecular motion); V2/2 is the directed kinetic energy per unit mass (with V as the mag­nitude of the velocity vector, a function of position and time in the field); and gz is the potential energy due to a uniform gravity field (assumed to act in the ver­tical direction—i. e., the z-direction in three-dimensional space). z is assumed to be measured from a convenient datum plane such as the earth’s surface. This notation is chosen to conform to that used most often in textbooks and other publications describing compressible-fluid flows.

To complete the statement of the First Law of Thermodynamics, we must provide models for the heat transfer to the control volume and the rate of work done by the control volume on the surroundings as indicated by the terms to the right of Eq. 3.39. Heat transfer may occur in the following two ways:

• internal heat release within the control volume such as by combustion, QINT

• heat transfer by conduction across the surface of the control volume, represented in terms of local conditions as:

Qcond = Я ¥S, (3-41)

S

where Q is the heat-transfer rate across the surface per unit surface area and Qcond is defined as the total heat-transfer rate to the control volume due to conduction from the surroundings. Heat transfer by radiation is not considered here, but it may be of crucial importance in problems in which temperatures are high (e. g., in the flow around a spacecraft reentering the earth’s atmosphere). Transfer of energy by convection across the boundaries of the control volume was accounted for in the surface integral (i. e., the third term in Eq. 3.39).

It remains to provide models for the rate of work done by the control volume on the surroundings. This work rate may arise from the following three sources:

1. Machine work (sometimes called “shaft work”) done internally within the control volume but carried by mechanical linkage through the control surface (e. g., a turbine or compressor connected to an external device by a rotating shaft). Let WM denote the mechanical work rate done by the fluid inside the control volume, where the dot over the “ W” denotes “time rate of change.” WM traditionally is assumed to be positive when it represents work done on the surroundings. Hence, it appears in the energy equation with a negative sign, as shown on the right side of Eq. 3.39.

2. The rate of work done at the control surface due to surface stresses, which has two parts. The part due to stresses tangent to the surface usually are due to the effects of viscosity. We denote the viscous-work-rate term by the symbol WY, which represents the work rate done on the fluid within the control volume by viscous forces acting at its bounding surface. The second part is due to the normal stresses, usually related to the pressure forces. Multiplying the pressure force on the surface per unit area, – pn, by an infinitesimal surface area, dS, yields a force that may be represented as a vector everywhere perpendicular to the control surface by multiplying this force by the outward pointing unit normal vector—namely, – pndS. Recall that force times distance in the same direction equals work. The work rate, then, is the force times the rate of change of dis­tance in the same direction—that is, the force times the velocity component in the direction of the force (the convenience of using a “rate” equation is evident here). However, because – pndS is a vector, taking the dot product of V with this vector results in multiplying the pressure force by the component of the velocity vector in the direction of this force. Thus, – p(V • n)dS is the required work rate due to normal pressure acting at the control surface. Then, the total work rate done on the system by normal surface tractions is given by:

-ДО p(V*n)dS.

S

3. The rate of work done on the fluid within the control volume by body forces. This term may be represented by:

jjj (pMV). V,

where b is the body force per unit mass and the dot product with the velocity vector yields the rate of work.

Assembling all of these terms and dropping the potential energy term (negli­gible in most aerodynamic problems) gives the general energy equation, Eq. 3.42:

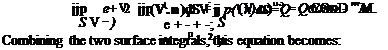Equation 3.42 may be expressed in a simpler form that is valid for a large class of aerodynamics problems by restricting the range of interest to steady flows with negligible viscous work, no combustion, negligible body-force effect, and negligible changes in potential energy. Then, the preceding equation simplifies to:

The various special forms of the energy equation that we use are summarized in Table 3.4.

Table 3.4. Energy equation in control-volume form

Now, recall that the thermodynamic state variable enthalpy, h, is defined by h = e + р/р, so that this equation becomes:

(3.44)

Defining the stagnation enthalpy as h0 = h + V/2, Eq. 3.44 may be written as:

For an ideal gas, the internal energy is proportional to the (absolute) tempera­ture. Therefore, we write e = cvT, where cv is the specific heat at constant volume. Also, remembering from the equation of state that the ratio р/р = RT, then h is also proportional to the temperature. Thus, it is typical to write h = cp T, where cp is the specific heat at constant pressure. In many situations, it is possible to assume that the two specific heats are constants independent of the temperature. We then speak of a calorically perfect gas. There exist cases in which the temperatures are so high (especially in hypersonic flows) that such assumptions may not be valid. The stagna­tion enthalpy, h0 = cp, T0, is useful for later discussions. The subscript “zero” denotes stagnation conditions (i. e., zero velocity).

example 3.6 Given: Air flows steadily through a long constant-diameter pipe at a mass-flow rate of 2.0 kg/s. The stagnation temperature has the same value (120°C) at two stations some distance apart along the pipe. Between these two stations, 2,000 Nm/s of work are added to the flowing air. Assume one­dimensional flow through the pipe. There is no combustion between the stations. Ignore work due to body forces and change in potential energy.

Required: Find the rate of heat addition (or subtraction) between these two stations by conduction through the pipe walls.

Approach: Select a convenient control volume. If the control surface coincides with the inside of the pipe, then at the walls, the rate of work due to viscosity is zero—the shear stress is large, but the velocity precisely at the wall is zero. At the two ends, the velocity is essentially constant so that the shear stresses (which are proportional to velocity derivatives) are small. Thus, viscous work may be assumed to be negligible.

Solution: Choose the control volume shown here and apply Eq. 3.45, recalling that outflow is positive and inflow is negative. Substituting in this equation yields:

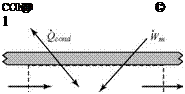J pV2C’pT0 )dS – J pVi(CpTo)dS = Q

Because the flow is one-dimensional and the pipe is of constant area:

P2V2(CPT0)2 A2 _ P1V1(CpT0)2 A1 = Cp (T02_ T0l)-

Now, T01 = T02 according to the given information, so that the left side of Eq. 3.25b is zero. It remains to apply the correct signs to the two terms on the right side. Recall that in the derivation of the energy equation, the machine work was defined as work done by the fluid. Because 2,000 Nm/s of work is added here, this number must enter the equation with a minus sign, so that:

0 = Qcond~ (-2,000) ^ Qcond = -2,°°°.

Because the QCOND term defines the rate of heat transfer to the control volume as positive, the resulting negative sign in the solution means that 2,000 Joules/s of heat is removed from the pipe between the two stations.

Appraisal: Because work is being done on the flowing air between the two stations and there is no change in stagnation temperature, the result that heat is being removed agrees with intuition. Notice that the numerical value of the stagnation temperature was not used. The only important fact was that the stag­nation temperature was constant. Thus, part of the given information was not required. For many problems encountered in the real world, not enough infor­mation is known (assumptions must be made) or too much information is known (irrelevant data must be discarded—but which?). This is where a physical under­standing of the problem and the equations becomes vital.

example 3.7 Given: There is a steady flow of air at a rate of 15 lbm/s through the compressor of a stationary gas turbine. The air enters at average conditions of T1 = 80°F and V1 = 10 ft/s and discharges at an average velocity of V2 = 90 ft/s. The compressor receives 500 HP of work from the turbine, while the heat loss from the compressor to the surroundings is 300 BTU/s. Assume that the work on the control surface is due only to pressure and ignore changes in potential – energy and body-force effects.

Required: Predict the average enthalpy of the air at the exit of the compressor.

Approach: Choose a suitable control volume that encloses the compressor. Use the steady-flow integral-energy equation with certain terms omitted.

Solution: Select the control volume shown here:

Now, p(V • n)dS = m ;therefore, for one-dimensional flow,

Recall that h = cpT and, from tables for air, cp = 0.24 BTU/lbm°F. Thus, on the left side of the equation, mh has the units of [lbm/s][BTU/lbm] = BTU/s. Because all terms in the equation must have the same units, arbitrarily adopt BTU/s as the standard to be used in this problem. Examining the units of the other terms in the equation and supplying appropriate conversion factors, the units of the following terms are:

BTU

s

Then, assemble these terms into Eq. 3.44, recognizing that heat is being trans­ferred from the control volume and work is being done on the gas within the control volume. Thus,

” “ qcond Wm

Solving, h2 = enthalpy of exit air = 133 BTU/lbm.

Appraisal: The resulting value for exit enthalpy implies an exit temperature of 94°F. The answer comes out positive (as it must be), and the magnitude of the exit temperature appears reasonable because it is greater than the inlet tem­perature. Note that we adopted the mass unit Ibm for this problem, as often is done in thermodynamics textbooks. The student is reminded that the slug is the compatible mass unit so that the conversion factor, gc = 32.2 lbm/slug, appears in the numerical evaluation.

Other Physical Laws in Control-Volume Form

We now have derived the control-volume equations that are needed throughout the book in numerous aerodynamics applications. Other physical laws are required
only occasionally in these applications. For example, the Second Law of Thermo­dynamics, Eq. 3.13, can be expressed readily in control-volume form. The procedure follows closely that used for the First Law. Similarly, the part of Newton’s Second Law pertaining to angular motion can be expressed readily in control-volume form following the same procedures described previously. Problems in the set of exercises at the end of the chapter provide the opportunity to test the student’s understanding by carrying out the details for some of these additional physical laws.