The equation of continuity or conservation of mass

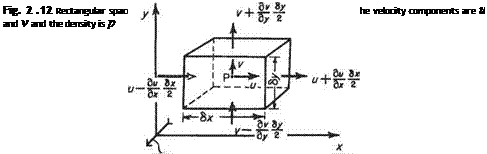
Consider a typical elemental control volume like the one illustrated in Fig. 2.8. This is a small rectangular region of space of sides 6x, 6y and unity, centred at the point P(x, y) in a fluid motion which is referred to the axes Ox, Oy. At P(x, y) the local velocity components are и and v and the density p, where each of these three quantities is a function of x, у and t (Fig. 2.12). Dealing with the flow into the box in the Ox direction, the amount of mass flowing into the region of space per second through the left-hand vertical face is:

mass flow per unit area x area

i. e.

(2.38)

The amount of mass leaving the box per second through the right-hand vertical face is:

(2.39)

The accumulation of mass per second in the box due to the horizontal flow is the difference of Eqns (2.38) and (2.39), i. e.

(2.40)

Similarly, the accumulation per second in the Oy direction is

(2.41)

so that the total accumulation per second is

As mass cannot be destroyed or created, Eqn (2.42) must represent the rate of change of mass of the fluid in the box and can also be written as

d{p x volume)
dt

but with the elementary box having constant volume (8x 8y x 1) this becomes

dp

aiSx6y^1

Equating (2.42) and (2.43) gives the general equation of continuity, thus:

dp d{pu) d(pv) dt dx dy

This can be expanded to:

and if the fluid is incompressible and the flow steady the first three terms are all zero since the density cannot change and the equation reduces for incompressible flow to

du dv d~x + d~y~

This equation is fundamental and important and it should be noted that it expresses a physical reality. For example, in the case given by Eqn (2.46)

This reflects the fact that if the flow velocity increases in the x direction it must decrease in the у direction.

For three-dimensional flows Eqns (2.45) and (2.46) are written in the forms:

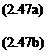dp dp dp dp (du dv dw

m + ufc+vdi+wte+p(fc+di+te)=0

du dv dw dx dy dz