THE LINEARIZED MODEL

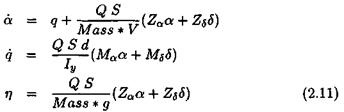The above model is linearized at a medium value r = 1 0 deg of the angle of attack. The following LTI model is obtained:

This model is essentially parameterized by the 4 stability derivatives MQ, Ms, Za and Zs – For the sake of simplicity, it was assumed that cos(a) « 1 in equation (2.7), so that Ma and Za correspond to the linearization of the nonlinear functions Cn(a,6,M) and Cm(a,6,M) with respect to a. On the other hand, Ms and Zs coincide with the quantities dn and dm in equation (2.9).

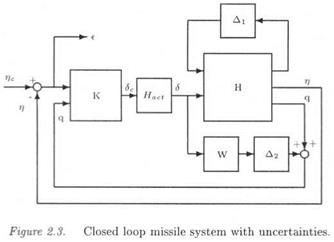
The issue in the following will be to analyze the local stability and performance properties of the closed loop missile in the presence of para­metric uncertainties in these 4 stability derivatives and in the face of neglected dynamics, namely a high frequency bending mode. To this aim, the parametrically uncertain missile model will be first transformed into a standard LFT structure Fu(H(s),Ai), where Ді gathers the un­certainties in the stability derivatives. On the other hand, the bending mode is represented by an additive model perturbation ДгЫ and its template 1/ W(5) is extracted from (Reichert, 1992; Balas and Packard, 1992). The uncertain closed loop missile is presented in Figure 2.3, where K(s) represents the missile autopilot. Note that the weights in the sta­bility derivatives are chosen as 5 %. In the context of Д» control, the frequency domain performance is defined through the sensitivity func­tion S, i. e. the transfer between the commanded acceleration r)c and the tracking error e = r)c — rj.