The stream function and streamline
1.3.2 The stream function у/
Imagine being on the banks of a shallow river of a constant depth of 1 m at a position О (Fig. 2.14) with a friend directly opposite at A, 40 m away. Mathematically
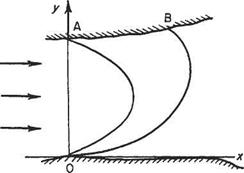
Fig. 2.14
the bank can be represented by the Ox axis, and the line joining you to your friend at A the Оу axis in the two-coordinate system. Now if the stream speed is 2ms-1 the amount of water passing between you and your friend is 40 x 1 x 2 = 80 m3 s-1 and this is the amount of water flowing past any point anywhere along the river which could be measured at a weir downstream. Suppose you now throw a buoyant rope to your friend who catches the end but allows the slack to fall in the river and float into a curve as shown. The amount of water flowing under the line is still 80 m3 s-1 no matter what shape the rope takes, and is unaffected by the configuration of the rope.
Suppose your friend moves along to a point В somewhere downstream, still holding his end of the line but with sufficient rope paid out as he goes. The volume of water passing under the rope is still only 80 m3 s-1 providing he has not stepped over a tributary stream or an irrigation drain in the bank. It follows that, if no water can enter or leave the stream, the quantity flowing past the line will be the same as before and furthermore will be unaffected by the shape of the line between О and B. The amount or quantity of fluid passing such a line per second is called the stream function or current function and it is denoted by ф.
 |
 |
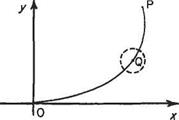
Consider now a pair of coordinate axes set in a two-dimensional air stream that is moving generally from left to right (Fig. 2.15). The axes are arbitrary space references and in no way interrupt the fluid streaming past. Similarly the line joining О to a point P in the flow in no way interrupts the flow since it is as imaginary as the reference axes Ox and Оу. An algebraic expression can be found for the line in x and y.
Let the flow past the line at any point Q on it be at velocity q over a small length Ss of line where direction of q makes angle /3 to the tangent of the curve at Q. The component of the velocity q perpendicular to the element Ss is q sin Q and therefore, assuming the depth of stream flow to be unity, the amount of fluid crossing the element of line Ss is q sin /3 x Ss x 1 per second. Adding up all such quantities crossing similar elements along the line from О to P, the total amount of flow past the line (sometimes called flux) is
which is the line integral of the normal velocity component from О to P.
If this quantity of fluid flowing between О and P remains the same irrespective of the path of integration, i. e. independent of the curve of the rope then fop q sin /3 dj is called the stream function of P with respect to О and
Note: it is implicit that V’o = 0.
Sign convention for stream functions
It is necessary here to consider a sign convention since quantities of fluid are being considered. When integrating the cross-wise component of flow along a curve, the component can go either from left to right, or vice versa, across the path of integration (Fig. 2.16). Integrating the normal flow components from О to P, the flow components are, looking in the direction of integration, either (a) from left to right or (b) from right to left. The former is considered positive flow whilst the latter is negative flow. The convention is therefore:
Flow across the path of integration is positive if, when looking in the direction of integration, it crosses the path from left to right.












