The streamline

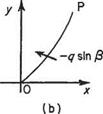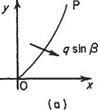
From the statement above, ipp is the flow across the line OP. Suppose there is a point Pi close to P which has the same value of stream function as point P (Fig. 2.17). Then the flow across any line OPi equals that across OP, and the amount of fluid flowing into area OPP^ across OP equals the amount flowing out across OP^ Therefore, no fluid crosses line PPi and the velocity of flow must be along, or tangential to, PP).

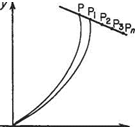Fig. 2.17

All other points P2, P3, etc. which have a stream function equal in value to that of P have, by definition, the same flow across any lines joining them to O, so by the same argument the velocity of the flow in the region of Рь P2, P3, etc. must be along PPi, P2, P3, etc., and no fluid crosses the line PPb P2,… ,P„. Since i/y, = ipPl = фр}=фр = constant, the line PPb P2,… P„, etc. is a line of constant ip and is called a streamline. It follows further that since no flow can cross the line PP„ the velocity along the line must always be in the direction tangential to it. This leads to the two common definitions of a streamline, each of which indirectly has the other’s meaning. They are:

A streamline is a line of constant ip

and/or

A streamline is a line of fluid particles, the velocity of each particle being tangential to the line (see also Section 2.1.2).

It should be noted that the velocity can change in magnitude along a streamline but by definition the direction is always that of the tangent to the line.