Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
TRANSFORMATION OF A VECTOR
Let v be a vector with the components
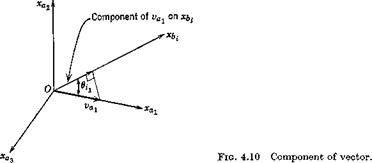
The component of vai in the direction of xb. is vai cos (6a) where ()a denotes the angle between 0bxb, and 0axai (see Fig. 4.10). Thus by adding the three components of va. in the direction of xb. we get
|
з
|
 |
|
 |
 |
and constitutes the required transformation formula. Its inverse readily reverses the transformation to give
