TRANSFORMATION OF THE DERIVATIVE OF A VECTOR

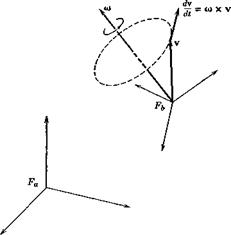
Consider a vector v that is being observed simultaneously from two frames Fa and Fb that have relative rotation—say Fb rotates with angular velocity a) relative to Fa, which we may regard as fixed. The rotation does not invalidate the argument of Sec. 4.4, so that

Уь = LbaVa (4‘4>3)

The derivatives of va and vb are of course

	"V		‘V
Va =	к	and v6 =	%
	-V		A.

where vx = (djdt)(vx ), etc. It is important to note that va and vb are not simply two sets of components of the same vector, but are actually two different vectors.

Now because Fb rotates relative to Fa, the direction cosines lti are changing with time, and the derivative of (4.4,3) is

Уь = ЬьЛ + (4-6’2)

or alternatively

У а ^аьУъ -6аїТ&

the second terms representing the effect of the rotation.

Since L must be independent of v, the matrix Lai) can readily be identified by considering the case when v6 is constant, see Fig. 4.12. For then, from the fundamental definitions of derivative and cross product, the derivative of v as seen from Fa is readily shown to be

dv — = w x v dt	(4.6,3)
The matrix equivalent of (4.6,3) is
У a = «Л	(4.6,4)

where

0 — <oz ft),

Fig. 4.12 Rotating vector of constant magnitude.

(4.6,5)

(4.6,6)

for all vh. Whence

and

^a ^ab^ba

Finally if the above argument be repeated with Fb considered fixed, and Fa having angular velocity —to, we clearly arrive at the reciprocal result Lba = -«A. (4.6,7) From (4.6,6) and (4.6,7), recalling that to is skew-symmetric so that toT = —to, the reader can readily derive the result

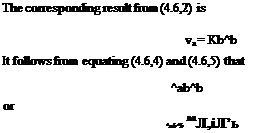From (4.6,2), (4.6,6), and (4.6,7) we have the alternative relations

^baFa ‘

(4.6,9)

with two additional permutations made possible by (4.6,8). A particular form we shall finally want for application is that which uses the components of va transformed into Fb, viz.

4,7 TRANSFORMATION OF A MATRIX

Equation (4.6,8) is an example of the transformation of a matrix the elements of which are dependent on the frame of reference. Generally the matrix of interest A occurs in an equation of the form

(4.7,1)

where the elements of the (physical) vectors u and v and of the matrix A are all dependent on the reference frame. We write (4.7,1) for each of the two frames Fa and Fb, i. e.

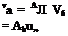(a)

(a) (4.7,2)

and transform the second to

By comparison with (4.7,2a) we get the general result