Unsteady Compressible Flows

1.2.1 The Full Potential Equation

The Euler equations represent conservation of mass, momentum and energy, assum­ing inviscid and adiabatic flow. Furthermore, for isentropic and irrotational unsteady flows, the governing equations become

dp д ( дФ д ( дФ д ( дФ dp

dt + дх P дх + д y P д y + ді P ді дї

boundary condition on a solid surface defined by F(x, y, z, t) = 0, can be as

dF д F

= + УФУF = 0, on F = 0 (5.42)

dt дї

where the velocity field of the surface points displacements has been replaced by the fluid velocity field, as both fields should be tangential to the surface.

To guarantee the continuity of the density and pressure across the vortex sheet, which is a slip line allowing for discontinuous tangential velocity only, the following condition must be imposed

= + V. У Г = 0 (5.43)

dt дї

where Г is the jump in the potential, Г = Ф + — Ф — and V is the mean tangential velocity. Note that the normal velocity component on the vortex sheet is continuous.

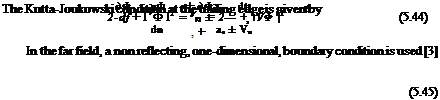where Vn is the normal component to the boundary and a0 is the speed fo sound of the undisturbed flow.

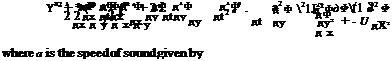Next, the governing equations are rewritten in non-conservative form and the discussion is limited to 2-D flows

The shock jump conditions of the potential formulation is given by

дФ дФ

< P > nt + < Рдх > Пх + < Рду > Пу = 0

On the shock, a normal vector is VS, where S&, у, t) is the surface of disconti­nuity. One finds

together with the condition of continuity of the potential

< Ф >= 0 (5.50)

The characteristics are obtained from the non-conservative form of the full po­tential equation as follows. Let, u = дФ/дх, v = дФ/ду and w = дФ/dt, hence

where we have made use of du/dt = dw/dx and dv/dt = dw/дy.

The eigenvalues of the two associated matrices are A = 0 and A = u ± a, and A = 0 and A = v ± a, respectively. The geometric interpretation of this result is that there exist two families of characteristic surfaces. Consider a point in the flow field and let it be the origin of the coordinate system. With respect to that point, one family, corresponding to A = 0, are planes that contain the t-axis. The other family are planes through the origin, that make an angle with the t-axis and envelop a cone of equation (see Fig. 5.9),

(x – ut)2 + (y – vt)2 = (at)2 (5.53)

The cross section of the cone by a plane t = const is a circle, centered at (ut, vt) and of radius r = at.

The origin is inside the circle when M0 < 1, and outside when M0 > 1. In the latter case, the tangents to the circle from the origin are the characteristic lines of the steady flow.

The zero eigenvalues can cause problems in the numerical solutions of the system of first order equations.

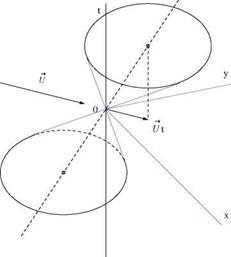
Fig. 5.9 Characteristic cone for the full potential equation