Unsteady Flow Past Thin Airfoils: Far Field Condition for Potential

The far field value of the potential is important as boundary condition when solving the unsteady flow potential equation, using finite differences, finite volumes or finite element methods. The leading term of the perturbation potential in the far field is due to the distribution of circulation Г along the x-axis. It is the only term for thin cambered plates (zero thickness). It reads

where (x, z) are the coordinates of a point where the potential is evaluated. See Fig. 5.3.

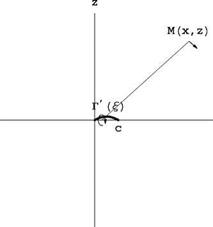Fig. 5.3 Far field evaluation of potential

The vorticity, dr, is in general singular at the leading edge x = 0 of the airfoil. Hence, in the numerical evaluation of the integral, it may be better to transform the expression by integrating by parts, to obtain

(5.31)

The first term vanishes at both limits, hence there remains

1 z

ф(х, z, t) = Г(£, t) 2 2

2n J0 (x — t)2 + z2