Validation: High Pressure Turbine Rotor

The present method was validated using a single stage turbine rig, represen­tative of a modern high-pressure turbine stage. It was designed in the course of the IMT Area 3 turbine project [12] and was used as a cornerstone in various European research programs [8]. In the ADTurB, and in the currently running ADTurBII program [4], the main emphasis is on aeroelastic effects. In the ADTurB program, the excitation of the rotor due to the stator wakes was stud­ied, with a special focus on the infhence of mechanical mistuning of the rotor blades. The resonant crossing of the 43rd engine order, corresponding to the excitation by the stator wakes, with the 1st torsional eigenmode was studied experimentally in this program. The data gathered in this effort will be used in the following to validate the current method for forced response calculations under mistuned conditions.

The operating point of the test vehicle is slightly transonic with exit Mach numbers just exceeding unity in the stator as well as in the rotor. The eigenfre – quencies of all rotor blades were determined by experimental modal analysis with the blades clamped to a massive supporting root block device. It was found that most blades 1T eigenfrequencies clustered around a mean value to within +/- 1.5%, while seven blades exhibited significantly lower eigenfre – quencies, deviating in excess of 5%. This large deviation was due to the fact that the blades were manufactured in different batches, which resulted in vari­ations of the geometric tolerances and possibly in the properties of the raw material used. As a consequence of this finding, these seven rogue blades were not included to calculate the mean frequency fmean that is used in the follow­ing analysis. The resulting mistuning parameter є = f/ fmean — 1 is shown in Fig. 1 for every blade, highlighting the severe mistuning of blades 5, 11, 17, 42 and 55 to 57. In the rig experiment, the blades are mounted on a disc, which adds significantly more flexibility to the blade root than the clamping device of the modal analysis. Furthermore, the disc introduces mechanical coupling between the individual blades. To account for these effects, the generalized stiffness used in the analysis is assumed to be 11% lower than the value re­sulting from the single blade FE calculation, and a coupling stiffness of 0.9% between each two neighboring blades is introduced into the system. These val­ues were deduced from the resonant frequencies measured in the rig test, i. e. after completion of the tests.

Sweeping the excitation frequency through the whole range of interest, the maximum response amplitudes of all blades were computed. A similar proce-

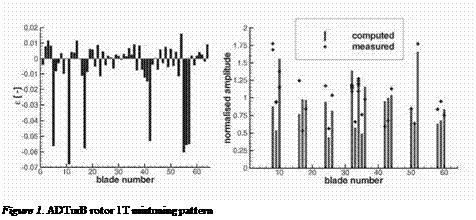Figure 2. Comparison of computed and measured maximum ADTurB rotor 1T / 43rd EO blade amplitudes

dure was used in the experiment, where the variation of excitation frequency was achieved by speeding up the rotor. This was done sufficiently slowly, so that the inflience of transient processes can be neglected. Experimentally de­termined blade amplitudes are available for 23 of the 64 rotor blades. Figure 2 shows the comparison of the resulting measured and computed maximum re­sponse amplitudes for all the blades that have experimental data available. The response amplitudes have been normalized using the mean value of the mea­sured peak amplitudes of all blades.

The measured data for the various blades was taken from a number of dif­ferent test runs, so that data from more than one run is available for a few of the blades. All the available data is included in this figure, so that the spread of the values for one blade, e. g. blade 32, gives an indication of the repeatability and measurement uncertainty of the experimental data. The figure indicates that the agreement between measured and computed data is quite acceptable. Not only is the mean response amplitude over the whole cascade matched well by the computation, but also the spread between the minimum and the maximum response of any blade is reproduced with good accuracy. Furthermore, in many instances the distribution of the amplitudes to the individual blades is shown by the computation in much the same manner as by the experiments.

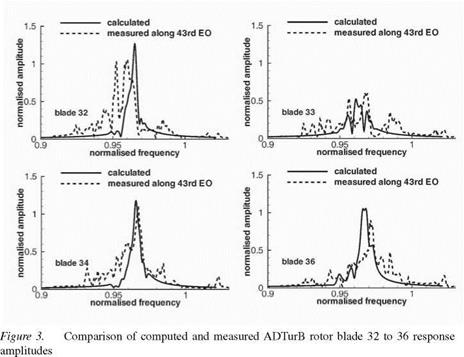
To further evaluate the ability of the current method to model the dominant effects of mistuning in this cascade, the amplitude distribution for the com­plete frequency sweep is compared to experimental values in Fig. 3. Here, the blades 32 through 34 and 36 are chosen for comparison, since the correspond­ing measured values on these blades were measured simultaneously in a single run, making them particularly well suited for such a comparison. The dashed

lines in Fig. 3 indicate the measured values, while the solid lines denote the computed results. The rotor speeds in this figure are non-dimensionalized us­ing the mean measured frequency that was used to determine the values of є in

Fig. 1.

Comparing the different graphs confirms the good agreement between the computed and the measured maximum amplitudes. Furthermore, the frequency at which this maximum occurs is also well met by the computation. Neverthe­less, some significant differences are also visible between the measured and the computed results. First, the computed distributions show much smoother curves than the measurements. It is not clear at this point if this behavior can be attributed to stochastic effects in the experiment or if there are deterministic phenomena at work that are not modeled by the current method. Secondly, especially blade number 32 shows two distinct maxima of almost equal mag­nitude, a fact that is not captured by the computation. In total, it can be con­cluded that the present method is capable of capturing the essential features of the mistuned cascade and is able to adequately reproduce the dynamic behavior in terms of resonant amplitudes.