Velocity components in terms of у/
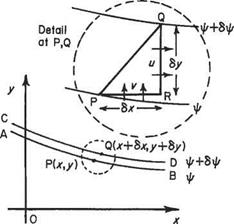
(a) In Cartesian coordinates Let point P(x, y) be on the streamline AB in Fig. 2.18a of constant ip and point Q(x + 8x, у + 6y) be on the streamline CD of constant ip + Sip. Then from the definition of stream function, the amount of fluid flowing across any path between P and Q = Sip, the change of stream function between P and Q.
The most convenient path along which to integrate in this case is PRQ, point R being given by the coordinates (x + 6x, y). Then the flow across PR = —v6x (since the flow is from right to left and thus by convention negative), and that across RQ = ибу. Therefore, total flow across the line PRQ is
![]() Sip = ибу — v6x
Sip = ибу — v6x
Now ip is a function of two independent variables x and у in steady motion, and thus
|
|
Fig. 2.18a дф/дх and дф/ду being the partial derivatives with respect to л: and у respectively. Then, equating terms:
и = дф/ду (2.56a)
and
v = —дф/дх (2.56b)
these being the velocity components at a point x, у in a flow given by stream function ф.
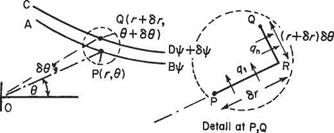
(b) In polar coordinates Let the point P(r, 6) be on the streamline AB (Fig. 2.18b) of constant ф, and point Q(r + 6r, 6 + 66) be on the streamline CD of constant ф + 6ф. The velocity components are qn and qu radially and tangentially respectively. Here the most convenient path of integration is PRQ where OP is produced to R so that PR = 6r, i. e. R is given by ordinates (r + 6r, 6). Then
6ф — – qt6r + qn(r + 6r)66 = —qt6r + qnr66 + qn6r66
To the first order of small quantities:
6ф = —qi6r + qar66 (2-57)
|
|
![]()
|
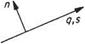
Fig. 2.19
|
But here ф is a function of (г, в) and again
|
these being velocity components at a point r, 0 in a flow given by stream function ф.
In general terms the velocity q in any direction л is found by differentiating the stream function ф partially with respect to the direction n normal to q where n is taken in the anti-clockwise sense looking along q (Fig. 2.19):
дф