AERODYNAMIC BEHAVIOR OF AIRPLANES

1- 3-1 Similarity Laws

The question of the mechanical similarity of two flows plays an important role in both the theory of fluid flows and the extensive testing procedures of fluid

mechanics. That is, given are two fluids of different physical properties, in each of which one of two geometrically similar bodies is located. Under what conditions are the two flow fields about the two bodies similar—in other words, under what conditions do they have a similar set of streamlines? Only in the case of mechanically similar flow fields is it possible to draw conclusions from the knowledge—which may have been obtained theoretically or experimentally—of the flow field about one body on the flow field about another geometrically similar body. To ensure mechanical similarity of flow fields about two geometrically similar, but not necessarily identical, bodies (e. g., two airfoils) in different fluids of different velocities, the condition must be satisfied that in each pair of points of similar position, the forces acting on two fluid elements must be similar in direction and magnitude. For the aerodynamics of aircraft, gravitation is of negligible influence and will not be considered for the establishment of similarity laws.

Mach similarity law First, let us consider the case of a compressible, inviscid flow. Here, except for inertia forces, only the elastic forces act on the fluid elements of a homogeneous fluid. For mechanically similar flows, obviously the relative density change caused by the elastic forces must be equal in the two flows. This leads to the requirement that the Mach numbers of both flows, that is, the ratios of flow velocity and sonic speed, should be equal. This is the Mach similarity law. The Mach number

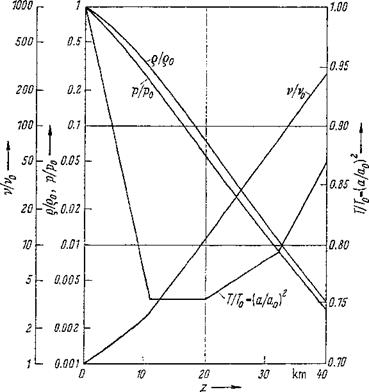Figure 1-2 Atmospheric pressure p, air density o, temperature T, speed of sound a, and kinematic viscosity v, vs. height z. From “U. S. Standard Atmosphere” [2].

is, therefore, a first important dimensionless characteristic number of flow processes. Since the effects of compressibility become noticeable for Ma> 0.3, as pointed out above, the Mach similarity law needs to be considered only above this limiting value. The fluid dynamic laws of an incompressible fluid can, therefore, be taken as the laws for very small Mach numbers with the limiting case Ma -> 0.

ill A*

Reynolds similarity law Let us now consider the case of an incompressible, viscous flow. Here, only inertia and viscous forces act on the fluid element. These two forces are functions of the following physical quantities: approach velocity V, characteristic body dimension /, density q, and dynamic viscosity /x of the fluid. The only possible dimensionless combination of these quantities is the quotient

where Re is called the Reynolds number. The ratio ju/g = v has been introduced above in Eq. (1-7) as the kinematic viscosity. This law was found by Reynolds in 1883 during investigations on the flow in pipes and is called the Reynolds similarity law.

If velocity and body dimensions are not too small, as in aeronautics, the Reynolds number is very large because of the very small values of v. This means physically that the friction forces are much smaller than the inertia forces in such cases. Inviscid flow (y ->0) corresponds to the limiting case Re-*00. The laws of flow with small viscosity often correspond quite well to those without viscosity. On the other hand, in many cases even a very small viscosity should not be neglected in the theory (boundary-layer theory).

For compressible flow with friction, mechanical similarity requires that the Mach and Reynolds similarity laws be satisfied simultaneously, which is very difficult to accomplish in experimental investigations. The Mach similarity law and the Reynolds similarity law govern decisively the whole realm of theoretical and experimental fluid mechanics and particularly the laws of aeronautics.

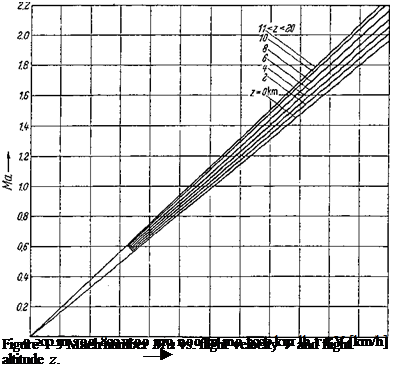
To give a convenient survey of the Mach and Reynolds numbers occurring in the aerodynamics of aircraft, the diagrams Fig. 1-3 and Fig. 1-4 have been drawn. They show these two dimensionless characteristic quantities versus flight velocity and flight altitude up to z = 20 km. Figure 1-3 shows that, at constant flight velocity, the Mach number increases with altitude because the sonic speed decreases, as was shown in Table 1-3. At an altitude of 10 km, the speed of sound has dropped to 300 m/s. At the same flight velocity, the Mach number at 10 km of altitude is about 10% larger than at sea level. This fact is important for the estimation of the aerodynamic properties of an airplane flying near the speed of sound.

The Reynolds numbers in Fig. 14 are those for a reference length of / = 1 m, where / may be the wing chord, fuselage length, or control surface chord. The Reynolds numbers of the diagram must be multiplied by a factor that corresponds to the reference length l in meters. Since the kinematic viscosity increases considerably with increasing height (see Table 1-3), the Reynolds number decreases

Figure 1-4 Reynolds number Re vs. flight velocity V and flight altitude 2.

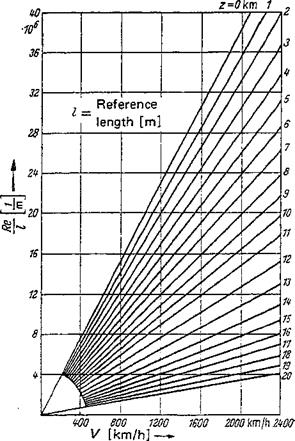
sharply with increasing height for a constant flight velocity, making airplane drag a particularly strong function of the height.