Aerodynamic centre

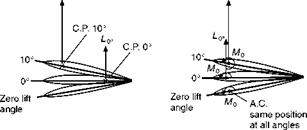
But something else of considerable importance arises from the differing effects of different reference points. For if about the leading edge there is a steady increase, and about a point near the trailing edge a steady decrease in the nose- down pitching moment, there must be some point on the chord about which there is no change in the pitching moment as the angle of attack is increased, about which the moment remains at the small negative nose-down value that it had at the zero lift angle (Figs 3.17 and 3.18).

This point is called the aerodynamic centre of the wing.

So we have two possible ways of thinking about the effects of increase of angle of attack on the pitching moment of an aerofoil, or later of the whole aeroplane; one is to think of the lift changing, and its point of application (centre of pressure) changing; the other is to think of the point of application (aerodynamic centre) being fixed, and only the lift changing (Fig. 3.19, overleaf). Both are sound theoretically; the conception of a moving centre of pressure may sound easier at first, but for the aircraft as a whole it is simpler to consider the lift as always acting at the aerodynamic centre. In both methods we really ought to consider the total force rather than just the lift, but

the drag is small in comparison and, for most purposes, it is sufficiently accu­rate to consider the lift alone.

At subsonic speeds the aerodynamic centre is usually about one-quarter of the chord from the leading edge, and theoretical considerations confirm this. In practice, however, it differs slightly according to the aerofoil section, usually being ahead of the quarter-chord point in older type sections, and slightly aft in more modern low drag types.

The graph in Fig. 3.18 (it can hardly be called a curve) shows how nearly the moment coefficient, about the aerodynamic centre, remains constant on our aerofoil at its small zero-lift negative value of about —0.09. This is further confirmed by the figures of CM given in Appendix 1 for a variety of aerofoil shapes.

The graphs tell us all we want to know about a particular wing section; they give us the ‘characteristics’ of the section, and from them we can work out the effectiveness of a wing on which this section is used.

For example, to find the lift, drag and pitching moment per unit span (about the aerodynamic centre) of an aerofoil of this section, of chord 2 metres at 6° angle of attack, and flying at 100 knots at standard sea-level conditions.

From Figs 3.13, 3.15 and 3.17, we find that at 6° –

CL = 0.6 CD = 0.028

CM = —0.09 about aerodynamic centre 100 knots = 51.6 m/s

1

Since ypV2 (or q) is common to the lift, drag and moment formulae, we can first work out its value –

L10° ^-10° Fig. 3.19 Centre of pressure and aerodynamic centre Two ways of looking at it.

q = |pV2 = і X 1.225 X 51.6 X 51.6 = 1631 N/m2

So lift = CL. q. S = 0.6 X 1631 X 2 = 1957 N drag = CD. q.S = 0.028 X 1631 X 2 = 91.3 N

pitching moment = CM. q. Sc = -0.09 X 1631 X 20 X 2

= -5872 N-m

But where is the aerodynamic centre on this aerofoil?

At zero lift there is only a pure moment, or couple, acting on the aerofoil, and since the moment of a couple is the same about any point, this moment, and its coefficient, must be equal to that about the aerodynamic centre, which we shall call CM Ac (sometimes written as CMO), and this by definition will remain the same whatever the angle of attack.

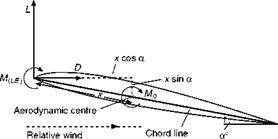
For all practical purposes we can assume that the aerodynamic centre is on the chord line, though it may be very slightly above or below. So let us suppose that it is on the chord line, and at distance x from the leading edge, and that the angle of attack is a° (Fig. 3.20).

The moment about the aerodynamic centre, i. e. CM Ac. q. Sc, will be equal to the moment about the leading edge (which we will call CM LE. q. Sc) plus the moments of L and D about the aerodynamic centre; the leverage being x cos a and x sin a respectively.

So

CM Ac ■ q ■ Sc = CM LE. q. Sc + CL. q. S. x. cos a + CD. q. S. x. sin a and, dividing all through by q. S,

CM ac ■ c = CM le ■ c CL ■ x. cos a + CD. x. sin a

••• X = C. (CM Ac – CM LE)/(CL cos a + CD sin a)

or, expressed as a fraction of the chord,

x lc = (CM. Ac – CM LE)/(CL cos a + CD sin a)

But the moment coefficient about the leading edge for this aerofoil at 6° is -0.22 (see Fig. 3.18), and CM Ac is -0.09 (Fig. 3.17),

CL = 0.6, cos 6° = 0.994, CD = 0.028, sin 6° = 0.10

So

x/c = (-0.09 + 0.22)1(0.6 X 0.994 + 0.028 X 1.10)

= 0.13/(0.60 + 0.003)

= 0.216

which means that the aerodynamic centre is 0.216 of the chord, or 0.432 metres, behind the leading edge, and so in this instance is forward of the quarter-chord (0.25) point.

Notice that at small angles, such as 6°, cos a is approx 1, sin a is nearly 0, so we can approximate by forgetting about the drag and saying that

x/c — (CM _ Ac — Cu _ le)/Cl

About the centre of pressure there is no moment, so (Distance of C. P. from L. E.)/c = —CM L£/(CL cos a + CD sin a)

= – CM. LE/CLaPProx

= +0.22/0.60 = 0.37

thus confirming the position of the C. P. as shown in Fig. 3.17.

All this has been explained rather fully at this stage; its real significance in regard to the stability of the aircraft will be revealed later.