BASIC SOLUTION: POINT DOUBLET

The second basic solution, presented in Eq. (3.13), is the doublet

<p = -£-n-v(T) (3.29)

4 я rf

A closer observation reveals that

for elements of unit strength. This suggests that the doublet element can be developed from the source element. Consider a point sink at the origin and a point source at 1, as shown in Fig. 3.4. The potential at a point P, due to these two elements, is

• =-—(———– —) (3.30)

4л |r| |r —1|/ V }

Now, bringing the source and the sink together by letting l—*0, o—>°° such that la-* fi, and ц is finite, the potential becomes

(7—»oo

As the distance l approaches zero,

|r| |r I| * r2

and the difference in length between |r| and |r -1| becomes

(|r —1| – |r|)—p/cos i?

FIGURE 3.4

The influence of a point source and sink at point P.

The angle # is between the unit vector Є/ pointing in the sink-to-source direction (doublet axis) and the vector r, as shown in the figure. Defining a vector doublet strength ц that points in this direction ц = ц e, can further simplify this equation:

pr

4яг3

Note that this doublet element is identical to the second term appearing in the general equation of the potential (Eq. (3.13), or Eq. (3.29)) if e, is in the n direction, thus

$doubie. 4лтз «w( 4лт) dn Ф^игсе (3.33)

For example, for a doublet at the origin, the doublet strength vector (fi, 0, 0) aligned with the x axis (e, = ex and § = в), the potential in spherical coordinates is

^„ ч fi cos 0

Ф(г, в, q>) = —(3.34)

Furthermore, in cartesian coordinates, the arbitrary orientation of ц can be expressed in terms of three generic unit doublet elements whose axes are aligned with the coordinate directions:

(fi, 0, 0) (0, fi, 0) (0, 0, fi)

The different elements can be derived for each of these three doublets by using Eq. (3.32) or by differentiating the corresponding term in Eq. (3.29) using Э/дп as the derivative in the direction of the three axes. The velocity potential due to such doublet elements, located at (jc0) y0, A)), is:

Taking 9/dn in the x, y, and z directions yields

/ d/9x i

ф<*’»г)I »£)

Equation (3.34) shows that the doublet element does not have a radial symmetry and it has a directional property. Therefore, in cartesian coordinates three elements are defined each pointing in the x, y, or z directions (see, for example, the element pointing in the x direction in Fig. 3.5). After performing

FIGURE 3.5.

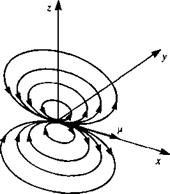Sketch of the streamlines due to a doublet pointing in the x direction (e. g., like a small jet engine blowing in the ц = (ft, 0, 0) direction).

the differentiation in Eq. (3.36) in the x direction the velocity potential is

Ф(х, У, z) = – у-(x – x0)[(x – *o)2 + (У – Уо)2 + (z – z0)2] 3/2 (3- 37)

4 л

The result of the differentiation in the у direction is

ф(*, y, z) = -y-(y-Уо)[(* – Xo)2 + (у – Уо)2 + (z – z0)2]-3/2 (3.38)

4 Jt

and the result in the z direction is

Ф(*. У, z) = –£-(z – Zo)l(-z – -«о)2 + (У ~ Уо)2 + (z – Zo)T3/2 (3.39)

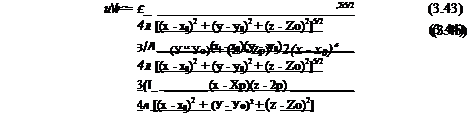The velocity field, due to an x-directional point doublet {ft, 0, 0) is illustrated in Fig. 3.5. The velocity components due to such an element at the origin are easily described in spherical coordinates:

ЭФ fi cos в 4r~ dr ~ 2 лг3	(3.40)
1 ЭФ n sin в Чв~гдв~ 4лг3	(3.41)
1 Зф n qv- . a з – 0 v r sin в 9<p	(3.42)

The velocity components in cartesian coordinates for this doublet at (x0, Уо» Zo) can be obtained by differentiating the velocity potential in Eq. (3.37):

|Ц(*о, Уо, z0)(x – x0) dl

ф(х, у, z) I ^ + ^ _ Л)2 + (2 _ Zq)2]3/2 <b(r v r = __L [ f*(x°>У°> Zo)(x-x0)dS 4л Js [(x – x0)2 + (y – y0)2 + (z ~ Zoff2 Ф(x у z) = ~— f ^Xo’ y°’ Zo)(-X ~Xo) dV 4 Jt Jy

Again, this basic point element can be integrated over a line /, a surface 5 or a volume V to create the corresponding singularity elements that can be used, for example, to construct panel elements. Consequently, these elements [e. g., for (/і, 0, 0)] can be established by the following integrals: