BASIC SOLUTION: VORTEX

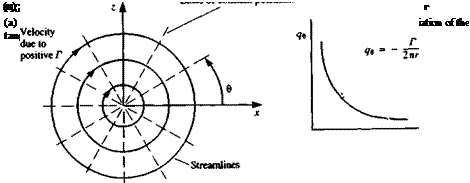
The general solution to Laplace’s equation as stated in Eqs. (3.13) and (3.17) consists of source and doublet distributions only. But as indicated in Section 3.6, other solutions to Laplace’s equation are possible and based on the vortex flow of Section 2.10 we shall formulate the velocity potential and its derivatives for a point vortex (the three-dimensional velocity field is then given by the Biot-Savart law of Section 2.11). Therefore, it is desired to establish a singularity element with only a tangential velocity component, as shown in Fig. 3.8a, whose magnitude will decay in a manner similar to the decay of the radial velocity component of a two-dimensional source (e. g., will vary with 1 /r):

qr = 0

qg = qe(r, в)

Substituting these velocity components into the continuity equation (Eq.

(1.35) ) results in qe being a function of r only

Яв = Яв(г)

For irrotational flow, substitute these relations into the vorticity expression to get

By integrating with respect to r, we get

rqe = const. = A

So the magnitude of the velocity varies with 1/r similarly to the radial velocity component of a source. The value of the constant A can be calculated by using the definition of the circulation Г as in Eq. (2.36):

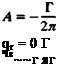Note that positive Г is defined according to the right-hand rule (positive clockwise), therefore, in the x-z plane as in Fig. 3.8 the line integral must be taken in the direction opposite to that of increasing 0. The constant A is then

and the velocity field is

(3.77)

(3.78)

As expected, the tangential velocity component decays at a rate of 1/r as shown in Fig. 3.86. The velocity potential for a vortex element at the origin can be obtained by integration of Eqs. (3.77) and (3.78):

Ф= q0rde + C = -^-e + C (3.79)

і 2 л

where C is an arbitrary constant that can be set to zero. Equation (3.79) indicates too that the velocity potential of a vortex is multivalued and depends on the number of revolutions around the vortex point. So when integrating around a vortex we do find vorticity concentrated at a zero area point, but with finite circulation (see Sections 2.9 and 2.10). However, if integrating q*dl around any closed curve in the field (not surrounding the vortex) the value of the integral will be zero (as shown at the end of Section 2.10 and in Fig. 2.11a). Thus, the vortex is a solution to the Laplace equation and results in an irrotational flow, excluding the vortex point itself.

Equations (3.77) to (3.79) in cartesian coordinates for a vortex located at (xo, 2o) are

Z-Zp

x —x0

Г z-Zp

2n(z-Zo)2 + (x-x0)2

_T_____ x-x0

2я (z — Zq)2 + (x — x0)2

To derive the stream function for the two-dimensional vortex located at the origin, in the x-z (or r-d) plane, consider the velocity components in terms of the stream function derivatives

__3W______

dr 2яг

law

Integrating Eqs. (3.83) and (3.84) and setting the constant of integration to zero yields

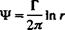(3.85)

and the streamlines where W = const, are shown schematically in Fig. 3.8a.