Construction of Flow Fields by the Superposition of Elementary Flow Functions

The sum of harmonic functions is itself a harmonic function. Thus, if we construct a flow field defined by a velocity potential ф^х, у, z) and another defined by ф2(х, у, z), these functions can be added to produce still another field. In general, if фи ф2,…,фп satisfy Laplace’s equation, then

V2c/> = 0,

where

Ф = І. Фг

1

The velocity of the new field thus constructed is given by

V = grad ф = grad £ ф„ (2-24)

1

Hence the velocities of the fields defined by фи ф2,…,фк add vectorially to produce the velocity defined by ф.

There are three elementary flow functions commonly used as “building blocks” for more complicated patterns. These functions are associated with purely rectilinear flow, purely tangential flow, and purely radial flow.

Rectilinear Flow

Consider the case in which the velocity vector is a constant given by V. If ф is taken to be zero at the origin, then

ф(х, у) = I V-fifR = их + vy;

и and v, of course, are the constant x – and у-components of V.

Similarly, the stream function is defined as zero at the origin. Since it was shown earlier that <Ц/ = —vdx + udy and и and v are constant, it follows immediately that

ф = uy — vx. (2-26)

Vortex

In polar coordinates r and в the curl of the velocity vector can be written as

щ and ur are the tangential and radial velocity components, respectively. For irrotational motion Eq. (2-27) must be equal to zero. If, in addition, the radial component of velocity ur is zero and ue is not a function of в, (2-27) becomes

dut _ dr r

Integrated, this equation becomes

uer = constant. (2-28)

Because the curl V is zero, the closed line integral of V*</R vanishes around every contour in the field with the exception of any contour enclosing the origin. At this singularity the velocity is infinite. Consider the evaluation of this line integral on a circle of constant radius R centered at the origin,

as shown in Fig. 2-3. If the value of this closed line integral is denoted by Г, then obviously

Г = 2nRue.

This equation is of the same form as (2-28) and, by comparison, the constant in (2-28) is taken to be T/2n. Hence for irrotational flow, with only a tangential component independent of angular position, the velocity is given as a function of the radius:

This type of flow is referred to as a point vortex; Г is the strength of the vortex and equal to the closed-line integral of the velocity about any contour enclosing the center of the vortex.

Although ф and ф for a vortex can be obtained by application of vector

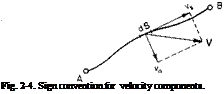
analysis, possibly it is clearer to think of the change in ф and ф between two points A and В as being obtained from the line integrals

в

vs dS,

I

ф(В) – ф(А) =j„dS;

vs and v„, in Fig. 2-4, are the velocity components directed along and normal to dS, respectively; v„ is shown in the positive sense, as previously discussed.

Consider (2-31) as applied to a vortex. This integral evaluated along a radial line from the origin is zero because и,, the velocity along the path of integration, is zero. Hence ф for a vortex is a function only of 6. If r is held constant, then (2-31) becomes

= — [0(B) – в(А)].

If 6(A) is taken to be zero and 6(B) is any general angular position, the velocity potential for a vortex can be written

Thus the equipotential lines are rays emanating from the center of the vortex.

In a similar manner it can be seen that when evaluated along a constant radius the integral of (2-32) is zero because the velocity normal to the arc is zero. Hence іjj can be obtained immediately by integrating along a radius. If A and В lie on the same radius, then

= _л, пш

In R{A)

If ф(А) is arbitrarily taken to be zero and R(A) is denoted by a, then for any general radius r

The signs of (2-33) and (2-34) are dictated by the choice of positive coordinate directions.

Source

A source flow is the counterpart of a vortex. The flow is irrotational but has only a radial component of velocity. This component is assumed to be independent of 0 so that, from (2-27), the curl V is obviously zero.

In polar coordinates the divergence of the velocity vector can be written

For the source, since щ = 0, (2-34), in order to satisfy continuity, becomes

dur ur

dr r

or

urr = constant.

Thus in the case of the source the radial velocity is of the same form as the tangential velocity for the vortex. The strength of the source Q is defined as the line integral (2-32) enclosed around the origin. For a source it therefore follows that

” 2nr

The source strength Q is equal to the flux of fluid passing through any
circle of radius r enclosing the origin, hence can be regarded as the flux emanating from the singularity at the origin.

Application of (2-31) and (2-32) results in the following stream function and velocity potential for the source.

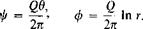(2-37)

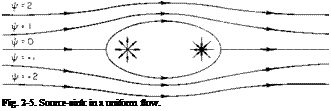It is possible, by combining the uniform rectilinear flow with sources and vortices, to produce flows of varying geometries; for example, by placing a

source and a sink (a source of negative strength) in line with a uniform flow we obtain the streamline pattern shown in Fig. 2-5. Because the conditions that define a streamline are the same as the boundary conditions that must be satisfied at a solid boundary, it follows that any streamline can be

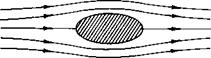
Fig. 2-6. Formulation of closed body or flow over a mound.

replaced by a solid boundary without altering the streamline pattern outside the boundary. Thus the flow of Fig. 2-5 can be made to represent the flow around the two-dimensional body defined by the ф = 0 line, or it might represent flow over a gentle mound represented by the ф = 1.0 line. These conditions are illustrated in Fig. 2-6.

The three elementary flow functions are summarized in Fig. 2-7.

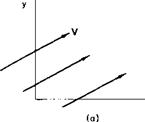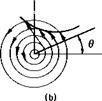Fig. 2-7. Elementary flow functions: (a) uniform rectilinear flow: v = constant, ф = их + try,
ф =uy — vx; (b) vortex; ue = T/2nr, itr = (),ф = Гв/2п, ф = — (Г/2гг) In г; (с) source: щ = О,
ur = Q 2nr, ф = (Q/2n) In г, ф = Q0/2n.