Energy Theorem

The energy theorem relates work and heat transfer to the flux of energy, both kinetic and thermal, through a control volume in a manner similar to the relation between the force and flux of momentum expressed in the momentum theorem. It is an adaptation of the first law of thermodynamics to fluid mechanics and follows directly from the first law.

If a system is defined as the fluid contained within a fixed control surface S, the rate at which heat is transferred into the system plus the rate at which work is performed on the system must equal the sum of the net flux of energy out of the system and the instantaneous rate of change of energy of the fluid particles contained within S.

In the first integral of Eq. (2-7), which represents the rate at which heat is transferred into the system, к is the coefficient of thermal conductivity. The second integral represents the rate at which surface stresses т work on the system; W is the power added to the system.

For the particular case in which viscous shearing stresses can be neglected the pressure forces are normal to the control surface so that the second integral on the left side of (2-7) becomes

jj [pe + /?)(V*n) — kn-VT] dS.

In addition, if the flow is steady, the first integral on the right side of (2-7) vanishes and (2-7) reduces to

The specific energy e is given as the sum of the intrinsic thermal energy and the kinetic energy

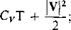(2-9)

Cv is the specific heat at constant volume. By substituting (2-9) and the equation of state p = pRT into (2-8) and recalling that Cp = R + Cv, we find that Eq. (2-9) becomes

The universal gas constant is R and Cp is the specific heat at constant pressure. Equation (2-8) is the energy theorem for the steady flow of an inviscid fluid that obeys the perfect gas laws. In words, it can be stated that the power added to a system must equal the net rate of flow of enthalpy (pCpT), kinetic energy (p|V|2/2), and heat out of the system.

The application of the momentum and energy theorems to the aero­dynamics of V/STOL aircraft will become apparent as the material in later chapters is developed.

Euler’s Equations of Motion

In the absence of body forces the momentum theorem for an inviscid fluid assumes the form

Application of Gauss’s theorem to this equation leads to

Because the volume is arbitrary, it follows that the integrand must satisfy the equation identically. By using the condition for conservation of mass expressed by Eq. (2-1) we obtain

(£ + v’,p)v -(2‘U)

The differential operator in parentheses is referred to as the substantial derivative with respect to time; it represents the rate of change as a particle moves along a streamline.

s. „ a>

To prove that this is so, consider the x-component of velocity u. In general, и is a function of x, y, z, and t so that

, , du, du, du,

du = — dt + — «X + — dy + – г – dz

dt dx dy dz

du <3m (3 m dx du dy du dz

dt dt dx dt dy dt dz dt

Because m = dx/dt, v = dy/dt, and и’ = dz/dt, it follows that

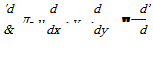
du

dt

‘d_

Jt

The first term in parentheses is referred to as the local acceleration. It is the rate of change of the м-velocity because of a temporal change in the flow field. The second term (V-V)m is the convective acceleration of the fluid particle caused by its changing position in the flow field.

In rectangular coordinates Eq. (2-11) is written

du du du du

— – 1-М — h » ,– h VT — =

dt dx dy dz

dv dv dv dv

—– b M— h c-—b VI’ — =

dt dx dy dz

dw dw dw dw ~dt+Ute+V^+WTz =

Equation (2-11) is the partial differential equation governing the flow of

an inviscid flow.

The vorticity vector eo is equal to the curl of the velocity vector:

to = V x v.

The behaviour of this vector quantity in an inviscid, incompressible flow can be found by taking the curl of both sides of Eq. (2-11);

dto 1

— + (V-V)© = —V X Vp.

dt p

The curl of the gradient of a scalar is identically zero. Thus

(2-13)

The substantial derivative of the vorticity vector со is equal to zero. Hence, as a function of (x, y, z, t), со must be a constant. For the specific case of a steady flow, uniform at some location in the field (usually infinitely far removed from the body), this constant must be zero. Hence everywhere in the flow field

со = 0. (2-14)

It must be remembered that the above holds only for a steady, inviscid, incompressible flow.

Velocity Potential

From the foregoing we have two conditions on the velocity vector of an incompressible inviscid flow:

curl V = 0, (2-15)

div V = 0. (2-16)

Now, by expressing the velocity vector as the gradient of a scalar function ф we find that (2-15) is identically satisfied. The scalar function ф is referred to as the velocity potential. Equation (2-16) leads to the condition that ф must be harmonic.

Thus, if

V = V</>, (2-17)

then from continuity considerations it must hold that

V20 = 0. (2-18)

A flow for which a velocity potential ф can be defined is known as a potential flow.

Stream Function

The stream function ф is defined only for two-dimensional or axi – symmetric flow. For two-dimensional, incompressible flow ф is defined as

dф = ^ndS; (2-19)

n is the unit vector normal to the differential arc length dS and is directed to the right as one faces in the direction of increasing dS. To investigate the ^-function further consider Eq. (2-19) in rectangular coordinates.

dS = |<Ж|,

. dy. dx

V = in + jn, dip — — vdx + udy.

In addition, because ф is a function of x and y,

дф дф

dф = – т— dx + dy. Y dx dy y

A comparison of these two expressions for dф produces the following relationships between ф and the velocity components:

It can be seen that to obtain the velocity component in a given direction the partial derivative of ф is taken in the direction normal to that of the velocity component and to the left as one looks in the direction of the velocity.

If we express the velocity in terms of ф, we find that the continuity con­dition (2-16) is identically satisfied. In order for curl V to equal 0, the following must hold:

VV = o.

Thus, to summarize, the velocity potential ф can be defined only if the flow is irrotational, that is, curl V = 0, and must be harmonic to satisfy continuity. The stream function satisfies continuity considerations and must be harmonic if the flow is to be irrotational.

A streamline is an imaginary line that defines the direction of flow so that at any point along the line the velocity is tangent to the line. Thus, if dy/dx is the slope of the line, it follows that

v _ dy и dx ’

dф was given earlier as dp = —vdx + u dy.

When the kinematic relationship along the streamline is substituted in the above, dф = 0 is the result. Thus lines of constant ф define the streamline pattern for a given flow field.

Equipotential lines are lines of constant ф. If ф is constant, it follows that

дф

dx + — dy dy

or

dy и

dx v

In a comparison of the slope of equipotential lines, as given by (2-23), with the slope of the streamlines defined by (2-23), it is apparent that the equi­potential lines are everywhere normal to the streamlines or lines of constant ф.