Equation of Motion in General Coordinates

Continuum equations of motion written in vector form are suitable for imple­menting the numerical solution of aerodynamical problems. In these equations the unknown vector U the flux vectors F, G and H, and the right hand side vector R are written as follows

Here, sxx, sxy, …, szz are the components of the stress tensor and qx, qy and qz are the components of the heat flux vector. Now, we can write the equation of motion in compact form as follows

OU OF OG OH

O t ^ O x ^ O y ^ O z

In many aerospace applications the Cartesian coordinates are not adequate to represent the surface equations of the body on which the boundary conditions are imposed. For this reason we have to write the equation of motion in body fitted coordinates which are generally referred as the generalized coordinates. Let the transformation from Cartesian coordinates xyz to the generalized coordinates ng1 be given as

X = Х(П, g; 1); У = y(|, g; і), z = , g, і)

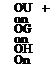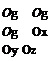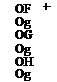With this information in hand, Eq. 2.49 is written in generalized coordinates in terms of the product of flux vectors with the metrics of transformation as follows (Anderson et al. 1984).

Shown in Fig. 2.6a, b are two different external flow regions: (a) wing upper surface and the boundaries of its computational domain, and (b) half a

fuselage and the computational domain transformed from xyz, Cartesian coordi­nates to ngf, generalized coordinate system. Both flow domains, after the trans­formation in ngf coordinate system, are mapped into the cube denoted by 12345678 for which the discretization of the computational domain becomes straight forward.

In Fig. 2.6, the ng surfaces of physical domain transforms into the square denoted with 1234, wherein, f coordinate of the physical domain is inclined with the body surface, i. e. it is not necessarily normal to the surface. After knowing one to one correspondence of the discrete points of both domains, we can numerically calculate the derivative terms for Пх, Пу, • ••, fz to be used for solving Eq. 2.50 in the discretized cube 12345678. There are quite a few numbers of literature pub­lished about the mesh generation and coordinate transformation techniques, however, two separate works by Anderson and Hoffman can be recommended for beginners and the intermediate level users (Anderson et al. 1984) and (Hoffman 1992).