Equations for Free-Flight Trim

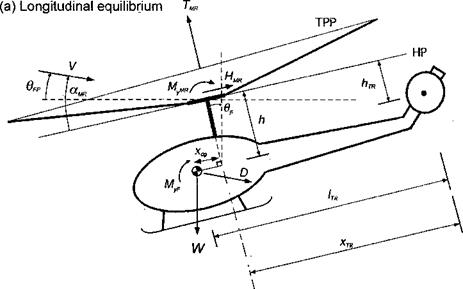
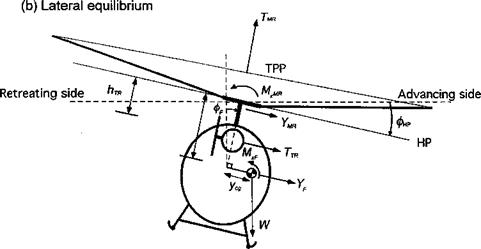
Figure 4.24 shows the forces and moments acting on the helicopter in free-flight. In the treatment of the trim problem, it is useful to decompose each of the components according to its origin. For example, the moment can be written in terms of the contributions from the main rotor (MR), fuselage (F), horizontal tail (HT), vertical tail (VT), tail rotor (TR), and other sources (O) as

M = Mmr + Mp + Мит + Myr + Mjr 4* Mo (4.102)

and similarly for the other force and moment components. The hub plane (HP) is used as the reference plane. The flight path (FP) angle is 6pp. It will be assumed that there is

Figure 4.24 Forces and moments acting on a helicopter in free-flight. (a) Longitudinal forces and moments, (b) Lateral forces and moments.

no side-slip angle, therefore the fuselage side force (YF) can be assumed negligible. Also, it will be assumed for simplicity that there are no contributions from the horizontal and vertical tails. For vertical force equilibrium

W—Tmr cose? cos фр+D sm6pp—HMR sin0f+YMr sinфр+YjR sin<Pf = 0.

(4.103)

For longitudinal force equilibrium a balance of forces results in

D cos Opp + HMR cos 6F — Tmr sin вр cos фр = 0. (4.104)

For lateral force equilibrium the tail rotor thrust, TPr, must be included to give

Ymr cos фр + TTR cos фр + TMR cos 9F sin фр = 0. (4.105)

For pitching moment equilibrium about the hub

MyMR + MyF — W(xcg cos вр — h sin 0/9 — D cos Gp(h cos 6F + xcg sin 0F) = 0.

(4.106)

For rolling moment equilibrium about the hub

MXMR + MXF – f – TTRhTR + W(h sin Фр – ycg cos фр) = 0. (4.107)

Finally, torque equilibrium about the shaft gives

Qmr — YTRlpR = 0. (4.108)

Using small-angle assumptions, the equilibrium equations can be reduced to the set

W-TMR = 0,

D + HMR — TMR0F = 0,

Y + TTR 4- Тшфр = 0,

Муш + MyF + W(h6p — xcg) — hD = 0,

Mxmr + MXF + W(hфp — ycg) – b TpRhjR = 0,

Qmr — TjrItr = 0.

The rotor thrust is simply the average of the blade lift during one revolution multiplied by the number of blades. Mathematically, this is stated as

дj p2n pR

TMr = ^ / dFzdf. (4.109)

J о Jo

The thrust coefficient can therefore be written as

Because of the complexity of the expressions for UP, UT, and в, this equation must usually be solved numerically. However, by assuming uniform inflow, that is, X(r, ф) = X = constant, Cd = CdQ, c = constant, and linear blade twist, we can obtain the result for the rotor thrust coefficient analytically. The result can be shown to be

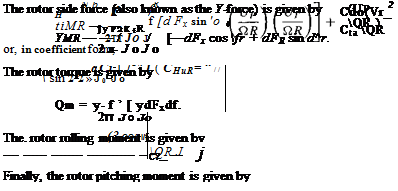In addition, the rotor torque, side force, drag force, and moments about the respective axes can be computed by a similar process. The rotor drag force (also known as the Я-force) is given by

Мут ~ ~Ът Jo Jo ydFz C°S ^d

Closed-form expressions for the latter quantities can also be derived.

Additional equations may be necessary. For example, two more equations should be added to determine the trim value of main rotor inflow Xmr and tail rotor inflow Xjr. These inflow equations should be solved together with all the other trim equations. For this purpose it is convenient to rewrite them so that all the terms are on one side of the equal sign. Using simple momentum theory for the main rotor (MR) gives

where їїmr cos amr = V/ QmrRmr and aMR is the disk AoA, for which setting aMR = a is usually reasonable. For the tail rotor (TR),

2-і/lijR 4" к

where fijR = V cos cctr/ QtrRtr and cijr is the disk AoA of the tail rotor (this will be zero if there is no side-slip angle).

The vehicle equilibrium equations, along with the inflow equations, can then be written in the form F(X) = 0, where X is a vector of rotor trim unknowns defined as

X = [0o 0c 0s mr ^tr 0F фр]т, (4.120)