Equations of Motion, Initial Conditions, Boundary Conditions, and Similarity Parameters

4.3.1 Transport of Momentum

Governing Equations. Momentum transport is described by means of the Navier-Stokes equations. Consider, for two-dimensional flow, the equation for momentum transport in ж-direction

(4.27)

The first term on the left-hand side represents the rate of increase of momentum in the unit volume with time, the second and third the gain of momentum by convective transport. On the right-hand side the first term stands for the pressure force on the unit volume, the first bracket for the gain of momentum by molecular transport, and the second bracket for the gain of momentum by mass diffusion. This term usually can be neglected.

(4.28) The components of the viscous stress tensor r in eqs. (4.27) and (4.28) are for a compressible Newtonian fluid7

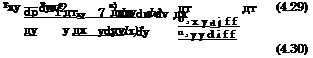The equation for the momentum transport in у-direction reads similarly, with the terms having the same meaning as before

dv 2 du dv

T»» = -2% + <3“-K) {&;+ fy) – (4 31)

Here we meet another transport property, the bulk viscosity к. It is con­nected to rotational non-equilibrium of polyatomic gases [3]. For practical purposes the formulation of this connection for air and its molecular con­stituents can be found in, e. g., [16]. For low-density monatomic gases к — 0. For the flow problems considered here we can assume in general к ^ p, and therefore neglect it.

7 Note that these components often are defined with opposite sign, e. g., Txx =

~ (§d – K)(fy + If)’ see’ e-g- M-

By adding to eq. (4.27) the “global” continuity equation multiplied by u, Sub-Section 4.3.3

we find the conservative formulation for the momentum transport in x – direction, see also Appendix A[32]

d(pu) d, 2 d, . .

+ -7^; {pu~ +p + txx) + — (pvu + тху) = 0. (4.33)

(pv2 + p + Tyy)

The conservative formulation for the momentum transport in y-direction is found likewise:

The shear stress exerted on the body surface, i. e., the transport of x- momentum in (negative) y-direction towards the surface, is found from eq. (4.30)

If distributed blowing or suction with a gradient in x-direction is not present, we arrive with dv/dxw = 0 at the classical wall-shear stress relation

For the surface pressure, which is a force normal to the surface, we do not have a relation, since it is an implicit result of the solution of the governing equations [17].

Mach Number, Reynolds Number, and Flow Boundary-Layer Thickness. We begin by comparing the convective x-momentum flux term and the pressure term in eq. (4.33):

22 pu pu

p pRT

The Mach number M is defined by

The magnitude of the Mach number governs compressibility effects in fluid flow, Chapter 6. Here we employ it only in order to distinguish flow types:

— M = 0: incompressible flow.

— M ^ Mcrit, lower: subsonic flow.[33] [34]

MCrit, lower ~ M ~ Mcrit, upper : transonic flow.

— Mcrit, upper ^ M ^ 5: supersonic flow.

— M ^ 5: hypersonic flow.

Hypersonic flow usually is defined as flow at speeds larger than those at which first appreciable high-temperature real-gay effects occur: M « 5. K. Oswatitsch defines hypersonic flow with M [18], see also Section 6.8. In

practice this means a Mach number large enough so that the Mach number independence principle holds.

Noting that the momentum flux is a vector entity, we compare now in a very schematic way the convective and the molecular ж-momentum flux in ж-direction in the first large bracket of eq. (4.33) after introducing the simple proportionality тхх ж p(u/L), which here does not anticipate the presence of a boundary layer

pu2 pu2 puL

— * ~пт = — = Де>

тхх ft(u/L) ft

and find in this way the Reynolds number Re. It can be interpreted as the ratio ‘convective transport of momentum’ to ‘molecular transport of momen­tum’ [4]. The Reynolds number is the principle similarity parameter governing viscous phenomena, Chapter 7.

The following limiting cases of Re can be distinguished:

— Re ^ 0: the molecular transport of momentum is much larger than the convective transport, the flow is the “creeping” or Stokes flow (see, e. g., [2, 19]): the convective transport can be neglected.

— Re ^ to: the convective transport of momentum is much larger than the molecular transport, the flow can be considered as inviscid, i. e., molecular transport can be neglected. The governing equations are the Euler equa­tions, i. e., in two dimensions eqs. (4.27) and (4.28) without the molecular
and mass-diffusion transport terms. If the flow is also irrotational, they can be reduced to the potential equation [6].

— Re = O(1): the molecular transport of momentum has the same order of magnitude as the convective transport, the flow is viscous, i. e., it is boundary-layer, or in general, shear-layer flow.[35]

We refrain from a discussion of the general meaning of the Reynolds number as a similarity parameter. This can be found in text books on fluid mechanics.

For Re = O(1) the convective transport of ж-momentum in x-direction pu? is compared now with the molecular transport of ж-momentum in y-direction Txy, anticipating a boundary layer with the (asymptotic) thickness S. We do this in the differential form given with eq. (4.27), assuming steady flow, and neglecting the second term of Tyx in Eq.(4.30)

u [ли

pu-oc

After rearrangement we obtain for the boundary-layer thickness S

S I p 1

— OC 4 ——– OC. ,

L у puL fReL

and, using the boundary-layer running length ж as characteristic length

This boundary-layer thickness is the thickness of the flow or ordinary boundary layer S = Sflow [19]. We will identify below with the same kind of consideration the thicknesses of the thermal, as well as the diffusion boundary layer, which are different from the flow boundary-layer thickness. The prob­lem of defining actual boundary-layer thicknesses is treated in Sub-Section 7.2.1.

Boundary Conditions. The Navier-Stokes equations (4.27) and (4.28) have derivatives of second order of the velocity components u and v in both ж – and y-direction. Hence we have to prescribe two boundary conditions for each velocity component. One pair (in two dimensions) of the boundary conditions is defined at the body surface, the other for external flow problems (far – field or external boundary conditions), in principle, at infinity away from the

body. For internal flows, e. g., inlet flows, diffuser-duct flows, etc., boundary conditions are to be formulated in an appropriate way.

We treat first the wall-boundary conditions for u and v, and consider the situation in both the continuum and the slip-flow regime, Section 2.3.

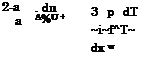For the tangential flow component uw at a body surface we get [20]

Here a is the reflection coefficient, which is depending on the pairing gas/surface material : 0 A a A 1. Specular reflection is given with a = 0, and diffusive reflection with a =1. Specular reflection indicates perfect slip, i. e., a ^ 0: (du/dy)w ^ 0. For air on any surface usually a = 1 is chosen. In Section 9.4 we will show results of a study on varying reflection coefficients.

The second term in the above equation

3 p dT

4 pT dx

in general is not taken into account in aerothermodynamic computation mo­dels. It induces at the wall a flow in direction of increasing temperature. On radiation-cooled surfaces with the initially steep decrease of the radiation – adiabatic temperature in main flow direction it would reduce the magnitude of slip flow. No results are available in this regard. However, the term can be of importance for measurement devices for both hypersonic hot ground – simulation facilities and flight measurements in the slip-flow regime.

After the mean free path, eq. (2.15), has been introduced into the se­cond term on the right-hand side, and after rearrangement, eq. (4.45) can be written in terms of the reference Knudsen number Knref = Xref /Lref

We find now in accordance with Section 2.3:

— the classical no-slip boundary condition for the continuum-flow regime:

Knref < 0.01 : uw =0, (4.47)

— and the slip-boundary condition eq. (4.45) for the slip-flow regime:

0.01 < Knref < 0.1 : uw > 0. (4.48)

The reference Knudsen number Knref must be chosen according to the flow under consideration. For boundary-layer flow, for example, the length scale Lref would be the boundary-layer thickness 5. Further it should be remembered that there are no sharp boundaries between the continuum and the slip-flow flow regime, Section 2.3.

The boundary condition for the normal flow component v at the body surface usually is

vw = 0. (4.49)

If there is suction or blowing through the surface, of course we get

vw =0 (4.50)

according to the case under consideration. Whether the suction or blowing orifices can be considered as continuously distributed or discrete orifices must be taken into account. For blowing through the surface also total pressure and enthalpy of the fluid, as well as its composition must be prescribed.

Far-field or external boundary conditions must, as initially mentioned, in principle be prescribed at infinity away from the body surface, also in down­stream direction. In reality a sufficiently large distance from the body is cho­sen. Because a flight vehicle induces velocity overshoots and velocity/total pressure defects in its vicinity and especially in the wake (due to lift, induced and viscous drag), far-field boundary conditions must ensure a passage of the flow out of the computation domain without upstream damping and reflec­tions. For this reason special formulations of the far-field boundary conditions are introduced, especially for subsonic and transonic flow computation cases.

In supersonic and hypersonic flows, depending on the employed compu­tation scheme, the upstream external boundary conditions can be prescribed just ahead of the bow shock if bow-shock capturing is used, or at the bow shock (via the Rankine-Hugoniot conditions, Section 6.1), if bow-shock fitting is employed. Then downstream of the body appropriate far-field boundary conditions must be given, as mentioned above.

The situation is different with two-domain computation methods, like coupled Euler/boundary-layer methods. Then external boundary conditions, found with solutions of the Euler equations, are applied at the outer edge of the boundary layer [4].