Flow Past Thin Wings

The above assumptions result in the existence of a perturbation potential ф(х, y, z) that governs the disturbance flow field (u, v, w) = Уф and verifies

The full velocity is V = Ui + Уф. This linear partial differential equation is not valid near Mach one, as was seen in 2-D. Unless otherwise stated, we will consider planar wings, i. e. wings whose base surface is in the (x, y) plane. Such a wing can be described by the equation z = f ± (x, y) where the plus sign corresponds to the upper surface and the minus sign to the lower surface. f± is small and of order e/c, d/c. Setting the wing at small incidence a amounts to adding to f± the shearing term a(cr – x), as was done in 2-D.

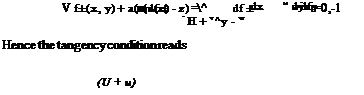The tangency condition requires that the flow be tangent to the thin wing, V. nlwing = 0. A vector, normal to the wing, has components

The transfer of the tangency condition from the actual wing surface to the nearby base surface yields, to first-order accuracy, the following result

w±(x, y, 0±) = U ^-d———- a^ (6.8)

The Bernoulli equation for a small perturbation yields the same result for pressure as was derived in 2-D, i. e. p = рж – p^Uu, hence the pressure coefficient is

u

Cp = —2 u (6.9)