‘Ideal’ Pressure Sensitive Paint

A perfect PSP should be completely temperature independent. According to Eq. (2.23), a temperature insensitive PSP should have such small activity energy ED for the oxygen diffusion process that the Stern-Volmer coefficient Bpoiymer is a

weak function of temperature over a certain range of temperature. However, since the excited-state decay rates of a luminophore are intrinsically temperature dependent, it is unlikely to develop an absolutely temperature-insensitive PSP whose the Stern-Volmer coefficients Apoiymer and Bpoiymer are constants. Instead,

researchers seek a so-called ‘ideal’ PSP exhibiting invariant temperature dependency at different pressures over a certain range of temperatures (Puklin et al. 1998; Coyle et al. 1999; Bencic 1999; Ji et al. 2000). Note that the term ‘ideal PSP’ does not accurately describe the invariant property of this special paint. Nevertheless, since this term has been used in the PSP community, we adopt it here and discuss its true meaning below.

Consider the Stern-Volmer relation in the following form

where 10(T) = I(p = 0,T) is the luminescent intensity at zero pressure (vacuum) and KSV(T) is related to the coefficients Apoiymer(T) and Bpoiymer(T) by

KSV(T ) = [ Bpolymer(T )/Apolymer(T )] ^ Pref. (3.2)

If the coefficients Apoiymer(T) and Bpoiymer(T) have the same temperature dependency, the Stern-Volmer coefficient KSV(T) becomes temperature independent. According to Eq. (2.23), this situation may occur under the conditions Ed ~ Enr and n ~ 1 over a certain range of temperatures. Therefore, for an ‘ideal’ PSP, the Stern-Volmer coefficient KSV(T) in Eq. (3.1), rather than the coefficients Apolymer(T) and Bpoiymer(T), is temperature independent.

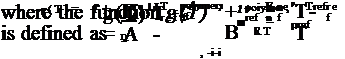Consequently, the Stern-Volmer relation in the form for aerodynamic application can be written as

and the coefficients Apolymer, ref and Bpolymer, ref are temperature independent given

the reference conditions. For an ‘ideal’ PSP, the Stern-Volmer relation Eq. (3.3) enjoys such similarity that it is invariant at different temperatures for the variable g( T )Iref /I. The temperature effect of PSP is concentrated in a single scaling

factor g(T); this similarity simplifies the temperature correction procedure for PSP.

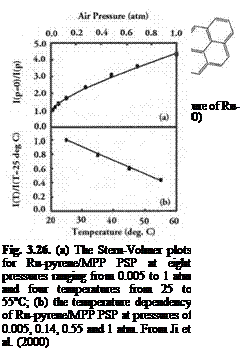Ji et al. (2000) developed a bichromophic molecule Ru-Pyrene for an ‘ideal’ PSP, which, as shown in Fig. 3.25, consisted of a covalently linked assembly of a Ruthenium (II) polypyridyl complex and Pyrene. They also synthesized the MPP acrylate polymer binder for Ru-Pyrene. Figure 3.26(a) shows the Stern-Volmer plots for the Ru-pyrene/MPP PSP at pressures ranging from 0.005 to 1 atm and temperatures from 25 to 55oC. The Stern-Volmer plots at different temperatures are collapsed onto a single curve. Figure 3.26(b) illustrates the temperature dependency of the Ru-Pyrene/MPP PSP at 0.005, 0.14, 0.55 and 1 atm, indicating that the temperature dependency of this PSP is independent of pressure.