INFLUENCE OF FUSELAGE ON Clft

The flow field of the body interacts with the wing in such a way as to modify its di­hedral effect. To illustrate this, consider a long cylindrical body, of circular cross sec­tion, yawed with respect to the main stream. Consider only the cross-flow component of the stream, of magnitude V/3, and the flow pattern which it produces about the body. This is illustrated in Fig. 3.17. It is clearly seen that the body induces vertical velocities which, when combined with the mainstream velocity, alter the local angle of attack of the wing. When the wing is at the top of the body (high-wing), then the angle-of-attack distribution is such as to produce a negative rolling moment; that is, the dihedral effect is enhanced. Conversely, when the airplane has a low wing, the di­hedral effect is diminished by the fuselage interference. The magnitude of the effect is dependent upon the fuselage length ahead of the wing, its cross-section shape, and the planform and location of the wing. Generally, this explains why high-wing air­planes usually have less wing dihedral than low-wing airplanes.

INFLUENCE OF SWEEP ON Clp

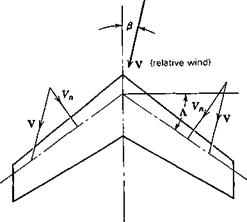
Wing sweep is a major parameter affecting C, . Consider the swept yawed wing illus­trated in Fig. 3.18. According to simple sweep theory it is the velocity Vn normal to a wing reference line (I chord line for subsonic, leading edge for supersonic) that de­termines the lift. It follows obviously that the lift is greater on the right half of the

wing shown than on the left half, and hence that there is a negative rolling moment. The rolling moment would be expected for small j8 to be proportional to

CJ(V2)right – (V2)left] = ClV2[cos2 (Л – P) – cos2 (A + (3)}

= 2CL/3V2 sin 2Л

The proportionality with C, and (3 is correct, but the sin 2Л factor is not a good ap­proximation to the variation with A. The result is a oc Q, that can be calculated by the methods of linear wing theory.