Integration for Power

The total torque can be obtained by integration in the same way that the total lift was:

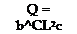R2a I (0, – ф,)фtrdr + cd I r’dr

a cd

-(0,-<МФ.+ —

2 4

Using expressions already derived, this becomes:

CT cdo

СЄ = Ст J~2+~tT

The first term in this equation is due to the combined effect of the rearward tilt of the incremental lift vectors in Figure 1.6 and is known as the induced torque coefficient. The induced torque coefficient could have been derived from the momentum equation by noting that the induced power is:

Pj = = T

and since it was earlier shown that CP was numerically equal to CQ:

CQi — Cp.= CT

This shows that the momentum theory and the blade element theory—at least for ideally twisted blades—produce the same expression for induced power. The second term in the equation for CQ is the profile torque coefficient and is due only to the drag of the blade elements. The Figure of Merit written in nondimensional terms is:

C„ CT/CJ2 _ fa (Cr/o)>n Cp C, – yj 2 Cs/c