Movement of centre of pressure

Pressure plotting experiments also show that as the angle of attack is altered the distribution of pressure over the aerofoil changes considerably, and in con­sequence there will be a movement of the centre of pressure. The position of the centre of pressure is usually defined as being a certain proportion of the chord from the leading edge. Figure 3.11 illustrates typical pressure distri­bution over an aerofoil at varying angles of attack. In these diagrams only the lift component of the total pressure has been plotted – the drag component has hardly any effect on the position of the centre of pressure. It will be noticed that at a negative angle, and even at 0°, the pressure on the upper surface near the leading edge is increased above normal, and that on the lower surface is decreased; this causes the loop in the pressure diagram, which means that this portion of the aerofoil is being pushed downwards, while the rear portion is being pushed upwards, so that the whole aerofoil tends to turn over nose first.

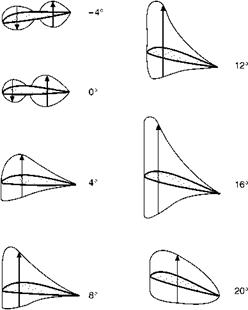So, even at the angle of zero lift, when the upward and downward forces are equal, there is a nose-down pitching movement on the aerofoil; as will be seen later this is a matter of considerable significance. Putting it another way,

How the lift distribution changes with angle of attack

at these negative angles the centre of pressure is a long way back – the only place where we could put one force which would have the same moment or turning effect as the distributed pressure would be a long way behind the trailing edge, in fact at zero lift it could not provide a pitching moment at all unless it were an infinite distance back – which is absurd. Perhaps a more sen­sible way of putting it is to say that there is a couple acting on the aerofoil, and a couple has no resultant and has the same moment about any point (see Chapter 1).

As the angle of attack is increased up to 16°, the centre of pressure gradu­ally moves forward until it is less than one-third of the chord from the leading edge; above this angle it begins to move backwards again.

Now during flight, for reasons we shall see later, the angle of attack is usually between 2° and 8° and is very rarely below 0° or above 16°. So, for the ordinary angles of flight, as the angle of attack of the aerofoil is increased, the centre of pressure tends to move forward.

Lift a pencil at its centre of gravity and it will lie horizontal; move the pos­ition at which you lift it forwards towards the point and the rear end of the pencil will drop: this is because the centre of lift has moved forwards as com­pared with the centre of gravity. Therefore if the aerofoil is in balance or ‘trimmed’ at one angle of attack, so that the resultant force passes through the centre of gravity, then the forward movement of the centre of pressure on the aerofoil as the angle of attack is increased will tend to drop still more the trailing edge of the aerofoil; in other words, the angle of attack will increase even more, and this will in turn cause the centre of pressure to move farther forward, and so on. This is called instability, and it is one of the problems of flight.

If we were to take the wing off a model aeroplane and try to make it glide without any fuselage or tail, we would find that it would either turn over nose first or its nose would go up in the air and it would turn over on to its back. This is because the wing is unstable, and although we might be able to weight it so that it would start on its glide correctly, it would very soon meet some disturbance in the air which would cause it to turn over one way or the other.

Curiously enough, in the case of a flat plate, an increase of the angle of attack over the same angles causes the centre of pressure to move backwards; this tends to dip the nose of the plate back again to its original position, and so makes the flat plate stable. For this reason it is possible to take a flat piece of stiff paper or cardboard, and, after properly weighting it, to make it glide across the room. If it meets a disturbance the centre of pressure moves in such a way as to correct it. Note that the flat piece of paper will only glide if it is weighted so that the centre of gravity is roughly one-third of the chord back from the leading edge. If it is not weighted the centre of pressure will always be in front of the centre of gravity, and this will cause the piece of paper to revolve rapidly.

The unstable movement of the centre of pressure is a disadvantage of the ordinary curved aerofoil, and in a later chapter we shall consider the steps which are taken to counteract it. Attempts have been made to devise aerofoil

Fig 3.12 Reflex curve near trailing edge shapes which have not got this unpleasant characteristic, and it has been found possible to design an aerofoil in which the centre of pressure remains practi­cally stationary over the angles of attack used in ordinary flight. The chief feature in such aerofoils is that the under-surface is convex, and that there is sometimes a reflex curvature towards the trailing edge (see Fig. 3.12); nearly all modern aerofoil sections have in fact got convex camber on the lower surface. Unfortunately, attempts to improve the stability of the aerofoil may often tend to spoil other important characteristics.