Rate of direct strain

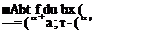
Following an analogous process we can also calculate the direct strains and their corresponding rates of strain, for example

The other direct strains are obtained in a similar way; thus the rates of direct strain are given by

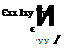Thus we can introduce a rate of strain tensor analogous to the stress tensor (see Section 2.6) and for which components in two-dimensional flow can be represented in matrix form as follows:

where ( ‘ ) is used to denote a time derivative.

2.7.2 Vorticity

The instantaneous rate of rotation of a fluid element is given by (a — /3)/2 – see above. This corresponds to a fundamental property of fluid flow called the vorticity that, using Eqn (2.71), in two-dimensional flow is defined as

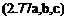da dp _ dv du dr dr dx dy

In three-dimensional flow vorticity is a vector given by

dw dv du dw dv du dy dz’ dz dx ’ dx dy)

It can be seen that the three components of vorticity are twice the instantaneous rates of rotation of the fluid element about the three coordinate axes. Mathematically it is given by the following vector operation

Q = Vxv (2.78)

Vortex lines can be defined analogously to streamlines as lines that are tangential to the vorticity vector at all points in the flow field. Similarly the concept of the vortex tube is analogous to that of stream tube. Physically we can think of flow structures like vortices as comprising bundles of vortex tubes. In many respects vorticity and vortex lines are even more fundamental to understanding the flow physics than are velocity and streamlines.