Second-order approximations

Using the Taylor series expansion in a small parameter є

(1-е)-1 = 1 + є + є2 + … (8.39)

the local Mach number expression (8.35) is converted from a rational form to a polynomial form,

M2 = MI 1 + (1 + ^M2 ) [2u+u2+v2 +w2] + V./2( 1 + ^M2 ) 4г/2 + … і (8.40)

where “…” denotes cubic terms O[М’Ж|u, v, w|3 ) and higher. Using the more general Taylor series ex­pansion

(1-е)6 = 1 – be + b(b-l)e2 + … (8.41)

the isentropic density and pressure (8.36), (8.37) likewise convert from power-law forms to the following polynomial forms.

Again, the “…” denotes cubic terms and higher.

To put the continuity equation into a polynomial form, we first need to expand the components of the normalized mass flux pV/рж Уж. These are obtained by multiplying the р/рж expression (8.42) in turn
with each component of V/V2, and then collecting the various powers and products of u, v,w.

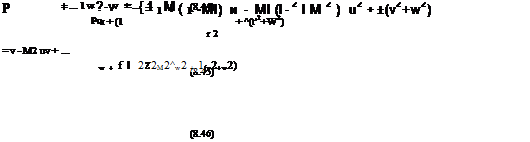+ … (1+u)

We next insert these mass flux component expressions into the compressible continuity equation, and also put the flow-tangency boundary condition in perturbation-velocity form.