Sources in compressible flow

In a compressible flow, with significant density variations, the source distribution a within the flow-field will in general be nonzero. This can be seen by computing a using the steady continuity equation (1.33).

V-(pV) = 0 pV – V + Vp ■ V = 0

V-V = (7 = –Vp-V (2.58)

p

Hence, a is nonzero wherever the density gradient has a component along the velocity vector. In the ir – rotational part of the flow outside the viscous layers, the density gradient is uniquely related to the speed gradient via the isentropic p(h) relation (1.69), and the adiabatic flow assumption of a constant total enthalpy

ho.

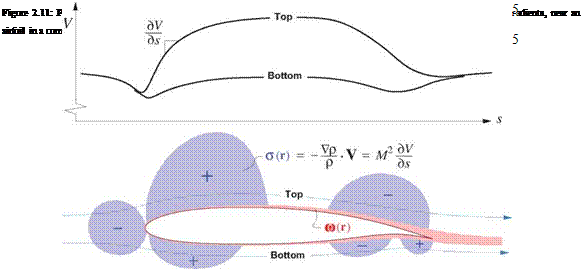
Vp _ J_Vh _ V(h0 – h2V2) _ V(^V2) _ VV

p у—1 h a2 a2 a2

Inserting this into (2.58) gives an alternative relation for a in terms of the streamwise speed gradient and the local Mach number,

where s was assumed to be parallel to V, with s being the arc length along a streamline. Figure 2.11 shows the typical positive and negative a field source distributions in the vicinity of a high-speed airfoil.

The source-superposition integrals (2.4) or (2.23) still correctly define the velocity field from the a field in this case, and indeed will be used in Chapter 8 to qualitatively investigate and explain compressible-flow behavior. However, because the a distributions near the airfoil are not necessarily compact and close to the airfoil, they cannot be lumped onto the airfoil surface as source sheets without seriously degrading the accuracy of the resulting velocity field. Hence, a must be treated as a volume quantity which makes the evaluation of the superposition integrals (2.4) or (2.23) computationally demanding.

A major consequence here is that quantitatively representing a compressible flow-field with sources and vortices is computationally cumbersome and quite impractical, at least in 3D. For this reason, CFD methods used for calculation of compressible flows typically use space-filling grids as shown in Figure 2.1 on which V(r) or <^(r) are defined by interpolation, and a or ш are not explicitly considered.

One exception is the case of small-disturbance compressible flows where the velocity everywhere departs only slightly from the freestream. In this case the effects of the nonzero a field can be captured by the Prandtl-Glauert coordinate transformation, which will be addressed in Chapter 8.