THE ANGULAR MOMENTUM

With components in FІг the angular momentum of the general deformable body is from (5.4,12c), on converting to matrix notation,

It is not convenient, as will be seen later, to have the angular momentum components referred to fixed axes. In fact we want its components along the axes FB, attached to the moving vehicle. From (4.6,10)

Rj — "Ь Фв®в) (5.4,14)

whence (5.4,13) gives the components of h in FB as

hj? = LBfhz =|bB/RjLJBRB dm + | JjbiRjLibG)bRb dm

Now the matrixR transforms according to the rule (4.7,4), so that =

RB and we get for hB

hB =|r#RBdm – l-JR/^tO/jR/^ dm (5.4,15)

When the body is rigid, R/; = 0, and the first term vanishes. [Note that JR* dm vanishes in any case because the origin is the mass center, see (5.4,116).] The second term of (5.4,15) is therefore identified as the “rigid-body component” of h, and the first term as the “deformation component.” To evaluate the second term, we note that шЕ = — lw (Since wxE = — R x со) and hence

(5.4,16)

Since (aB is constant with respect to the integration, we may write

‘ |®тД. в**>в f^m — – Fb^b (5.4,17)

JFB= – RBRB dm (5.4,18a)

(note the identity RR = RyRI — RRT). After expansion of (5.4,18a) and integration we get

(5.4,186)

The two notations for the elements of^ given in (5.4,186) are both traditional and in current use in flight dynamics literature. These elements are the

138 Dynamics of atmospheric flight moments and products of inertia, i. e.

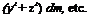
I.

Note that the inertia matrix transforms according to (4.7,4), so that for two reference frames FBi and Fb* we have

(5.4,20a)

For any 1Si, there always exists a transformation IіВіВг that produces a diagonal matrix B„ (see ref. 5.1). FB is then a set of principal axes, for which the products of inertia all vanish. When the vehicle has a plane of symmetry, then the x and z principal axes lie in it. If the body axes FB are obtained from the principal axes by a rotation є about Су, the elements of ■FB are found from (5.4,20a) to be

Ix = Ix cos2 e + Іг sin2 e

Iz = Ix sin2 Є + I cos2 e Jzx = W-,, – ht) sin hv = I„ = 0

where the subscript p denotes principal axes.

Let us denote the deformation component of h by

(5.4,21)

so that (5.4,15) gives the total angular momentum

Кв — Кв + ^выв

From (5.4,21) we can evaluate h)} as